题目内容
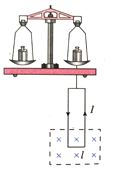
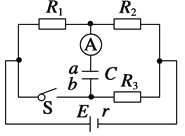
【题目】【加试题】如图甲所示,M、N为两块带等量异种电荷的平行金属板, ![]() 为板上正对的小孔,N板右侧有两平面荧光屏相互垂直放置,在两屏内分别取垂直于两屏交线的直线为x轴和y轴,交点O为原点,在y>0,0<x<d的区域有垂直于纸面向外的匀强磁场,在y>0,x>d的区域有垂直纸面向里的匀强磁场,两区域内有磁感应强度大小均为B,M板左侧电子枪随时间均匀发射出初速度可以忽略的热电子,所有电子经小孔
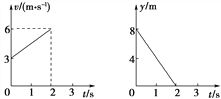
为板上正对的小孔,N板右侧有两平面荧光屏相互垂直放置,在两屏内分别取垂直于两屏交线的直线为x轴和y轴,交点O为原点,在y>0,0<x<d的区域有垂直于纸面向外的匀强磁场,在y>0,x>d的区域有垂直纸面向里的匀强磁场,两区域内有磁感应强度大小均为B,M板左侧电子枪随时间均匀发射出初速度可以忽略的热电子,所有电子经小孔![]() 进入两板间的电场加速后,从O点处小孔沿x轴正方向射入磁场,最后打在荧光屏上,使得荧光屏发亮,已知电子的质量为m,电荷量为e,M、N两板间所加的电压如图乙所示,电子通过MN的时间极短,且不计电子间的相互作用,求:
进入两板间的电场加速后,从O点处小孔沿x轴正方向射入磁场,最后打在荧光屏上,使得荧光屏发亮,已知电子的质量为m,电荷量为e,M、N两板间所加的电压如图乙所示,电子通过MN的时间极短,且不计电子间的相互作用,求:

(1)当两板间电势差![]() 时,电子在磁场中运动的轨迹为多长;
时,电子在磁场中运动的轨迹为多长;
(2)在一个周期内打在y屏上的电子数占总电子数的比例为多少;
(3)x屏上的亮线长度为多少。
【答案】(1) ![]() (2) 66.7% (3)
(2) 66.7% (3) ![]()
【解析】解:(1)根据动能定理,得![]()
电子在磁场中![]()
电子在磁场中运动的轨迹为![]()
(2)要使粒子打在y屏上,则半径r<d,即![]()
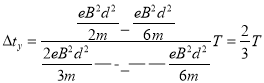
所以一个周期内打在y的粒子占比为66.7%
(3)分析可知,只有当![]() 时,即r≥d,粒子才能打到x屏上
时,即r≥d,粒子才能打到x屏上
当![]() 时,r=d,此时打在x屏上的坐标为x1=2d
时,r=d,此时打在x屏上的坐标为x1=2d
当![]() 时,
时, ![]() ,此时打在x屏上的坐标为
,此时打在x屏上的坐标为![]()
x屏上的亮线长度为△x=x2-x1= ![]()

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目