题目内容
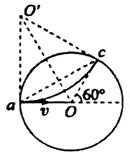
如图所示,分布在半径为![]() 的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里。电荷量为
的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里。电荷量为![]() 、质量为
、质量为![]() 的带正电粒子从磁场边缘
的带正电粒子从磁场边缘![]() 点处沿圆的半径
点处沿圆的半径![]() O方向射入磁场,离开磁场时速度方向偏转了
O方向射入磁场,离开磁场时速度方向偏转了![]() 角,试求:
角,试求:
(1)粒子做圆周运动的半径R;
(2)粒子的入射速度![]() ;
;
(3)若保持粒子的速率不变,从![]() 点入射时速度的方向顺时针转过
点入射时速度的方向顺时针转过![]() 角,粒子在磁场中运动的时间
角,粒子在磁场中运动的时间![]() 。
。

(1)如图所示,设正离子从磁场区域射出点为C,射出方向的延长线与射方向的直径交点为O,正离子在磁场中运动的轨迹![]() 是一段圆弧,它的圆心
是一段圆弧,它的圆心![]() 一定位于过入射点
一定位于过入射点![]() 且与入射方向垂直的直线上,由于正离子射出磁场的方向必沿圆弧
且与入射方向垂直的直线上,由于正离子射出磁场的方向必沿圆弧![]() 在C点的切线,故连线
在C点的切线,故连线![]() 必垂直于连线
必垂直于连线![]() ,又因为四边形的内角和为
,又因为四边形的内角和为![]() ,可推出
,可推出![]() ,即正离子在磁场区域中运动轨迹
,即正离子在磁场区域中运动轨迹![]() 弧对点
弧对点![]() 所张的圆心角为
所张的圆心角为![]() ,轨道半径
,轨道半径![]() …………4分
…………4分
 (2)粒子在磁场中运动时洛伦兹力提供向心力
(2)粒子在磁场中运动时洛伦兹力提供向心力
![]() ,解得
,解得![]() ………………4分
………………4分
(3)如果整个空间都充满了方向垂直于纸面向里的匀强磁场,正离子在纸面上做圆周运动的周期为![]() 由于轨道半径不变,当离子速度方向沿顺时针方向转
由于轨道半径不变,当离子速度方向沿顺时针方向转![]() 时,运动轨迹
时,运动轨迹![]() 弧所对圆心角仍为
弧所对圆心角仍为![]() 角,则正离子沿圆弧由
角,则正离子沿圆弧由![]() 点运动到
点运动到![]() 点所需时间
点所需时间
![]() ……………………………4分
……………………………4分
解析:
略

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里.电荷量为q、质量为m的带正电粒子从磁场边缘a点处沿圆的半径AO方向射入磁场,离开磁场时速度方向偏转了60°角,试求:
如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里.电荷量为q、质量为m的带正电粒子从磁场边缘a点处沿圆的半径AO方向射入磁场,离开磁场时速度方向偏转了60°角,试求: 如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里.电荷量为+q、质量为m的带电粒子从磁场边缘A点沿圆半径AO方向射入磁场,粒子离开磁场时速度方向偏转了60?角.求:
如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里.电荷量为+q、质量为m的带电粒子从磁场边缘A点沿圆半径AO方向射入磁场,粒子离开磁场时速度方向偏转了60?角.求: