题目内容
15.用m表示人造地球同步卫星的质量,h表示它离地面的高度,R0表示地球半径,g0表示地球表面处的重力加速度,ω0表示地球自转的角速度,则通讯卫星所受地球对它的万有引力大小是( )| A. | 0 | B. | $\root{3}{{R}_{0}^{2}{g}_{0}{ω}_{0}^{4}}$ | C. | $\frac{m{R}_{0}^{2}{g}_{0}}{({R}_{0}+h)^{2}}$ | D. | mg0 |
分析 由题地球的同步卫星的轨道半径为R=R0+h.根据地球的半径和地球表面的重力加速度,由重力等于万有引力,可求出地球的质量.
由向心力公式求解向心力
解答 解:在地球表面,由重力等于万有引力得mg=G$\frac{Mm}{{R}_{0}^{2}}$----①
在卫星位置,由重力等于万有引力得mg′=G$\frac{Mm}{({R}_{0}+h)^{2}}$----②
通讯卫星所受万有引力的大小F=ma=mg′.
同步卫星做圆周运动由万有引力提供向心力得:F=mω0 2(R+h)=mg′
所以F=mω0 2(R0+h)=$m\root{3}{{R}_{0}^{2}{g}_{0}{ω}_{0}^{4}}$=$\frac{m{R}_{0}^{2}{g}_{0}}{({R}_{0}+h)^{2}}$
故C正确,ABD错误.
故选:C
点评 本题为天体运动的典型题型,由万有引力提供向心力,再根据向心力的基本公式求解,解题过程中注意黄金代换式的应用

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
5. 截面为直角三角形的木块A质量为M,放在倾角为θ的斜面上,当θ=37°时,木块恰能静止在斜面上,如图甲.现将θ改为30°,在A与斜面间放一质量为m的光滑圆柱体B,如图乙,已知sin37°=0.6,cos37°=0.8,则( )
截面为直角三角形的木块A质量为M,放在倾角为θ的斜面上,当θ=37°时,木块恰能静止在斜面上,如图甲.现将θ改为30°,在A与斜面间放一质量为m的光滑圆柱体B,如图乙,已知sin37°=0.6,cos37°=0.8,则( )
 截面为直角三角形的木块A质量为M,放在倾角为θ的斜面上,当θ=37°时,木块恰能静止在斜面上,如图甲.现将θ改为30°,在A与斜面间放一质量为m的光滑圆柱体B,如图乙,已知sin37°=0.6,cos37°=0.8,则( )
截面为直角三角形的木块A质量为M,放在倾角为θ的斜面上,当θ=37°时,木块恰能静止在斜面上,如图甲.现将θ改为30°,在A与斜面间放一质量为m的光滑圆柱体B,如图乙,已知sin37°=0.6,cos37°=0.8,则( )| A. | A、B仍一定静止于斜面上 | |
| B. | 若M=2m,则A受到斜面的摩擦力为$\frac{3}{2}$mg | |
| C. | 若M=4m,则A受到斜面的摩擦力为$\frac{5}{2}$mg | |
| D. | 以上说法都不对 |
6. 如图所示,粗糙且绝缘的斜面体ABC在水平地面上始终静止.在斜面体AB边上靠近B点固定一点电荷,从A点无初速释放带负电且电荷量保持不变的小物块(视为质点),运动到P点时速度恰为零.则小物块从A到P运动的过程( )
如图所示,粗糙且绝缘的斜面体ABC在水平地面上始终静止.在斜面体AB边上靠近B点固定一点电荷,从A点无初速释放带负电且电荷量保持不变的小物块(视为质点),运动到P点时速度恰为零.则小物块从A到P运动的过程( )
 如图所示,粗糙且绝缘的斜面体ABC在水平地面上始终静止.在斜面体AB边上靠近B点固定一点电荷,从A点无初速释放带负电且电荷量保持不变的小物块(视为质点),运动到P点时速度恰为零.则小物块从A到P运动的过程( )
如图所示,粗糙且绝缘的斜面体ABC在水平地面上始终静止.在斜面体AB边上靠近B点固定一点电荷,从A点无初速释放带负电且电荷量保持不变的小物块(视为质点),运动到P点时速度恰为零.则小物块从A到P运动的过程( )| A. | 水平地面对斜面体没有静摩擦作用力 | |
| B. | 小物块的电势能先增大后减小 | |
| C. | 小物块所受到的合外力一直减小 | |
| D. | 小物块损失的机械能大于增加的电势能 |
4. 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中两物体( )| A. | 机械能均逐渐减小 | B. | 经最低点时动能相等 | ||
| C. | 均能到达半圆形槽右边缘最高点 | D. | 机械能总是相等的 |
5.质量为m的汽车,它的发动机额定功率为P,开上一倾角为α的坡路,摩擦阻力是车重的k倍,汽车的最大速度应为( )
| A. | $\frac{P}{mgsinα}$ | B. | $\frac{Pcosα}{mg}$ | C. | $\frac{P}{mg(k+sinα)}$ | D. | $\frac{Pcosα}{mg(k+sinα)}$ |
 在研究平抛运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=1.25cm,若小球在平抛运动途中的几个位置如图a、b、c、d所示,则小球平抛的初速度的计算式为v0=2$\sqrt{gl}$(用L、g表示),其值是0.7m/s (取g=9.8m/s2)
在研究平抛运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=1.25cm,若小球在平抛运动途中的几个位置如图a、b、c、d所示,则小球平抛的初速度的计算式为v0=2$\sqrt{gl}$(用L、g表示),其值是0.7m/s (取g=9.8m/s2)
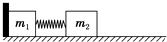 如图所示,两个木块的质量分别为m1=0.2kg、m2=0.6kg,中间用轻弹簧相连接放在光滑的水平面上,且m1左侧靠一固定竖直挡板.某一瞬间敲击木块m2使其获得2m/s水平向左的速度,木块m2向左压缩弹簧然后被弹簧弹回,弹回时带动木块m1运动.求:
如图所示,两个木块的质量分别为m1=0.2kg、m2=0.6kg,中间用轻弹簧相连接放在光滑的水平面上,且m1左侧靠一固定竖直挡板.某一瞬间敲击木块m2使其获得2m/s水平向左的速度,木块m2向左压缩弹簧然后被弹簧弹回,弹回时带动木块m1运动.求: