题目内容
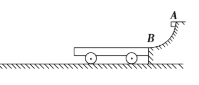
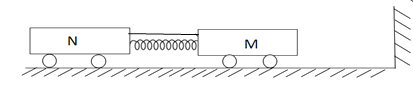
【题目】在光滑水平面上有两辆质量分别为
和
平板车M和N，它们用一根不可伸长的轻绳连接，轻绳处于绷紧状态，中间夹着一根处于压缩状态的轻质弹簧（弹簧与两小车不栓接），其弹性势能为27J。现用火烧断轻绳，M车和N车被弹簧弹开，弹簧恢复原长后，在M车的左端以与M车相同的速度放上一块质量为
的铁块，M车与铁块一起运动一段时间后，第一次与墙壁发生碰撞。已知铁块与M车之间的动摩擦因数
，M车足够长，使得铁块始终不能与墙相碰，M车与墙发生正碰，碰撞时间极短，碰撞过程无机械能损失。求
(1)弹簧恢复原长时两车的速度大小；
(2)从M车第一次与墙壁相碰到向左运动到最远距离的过程中，铁块相对M车滑行的距离；
(3)M车和墙相碰后所走的总路程。
【答案】(1)
；(2)1.4m；(3)1.25m
【解析】
(1)从烧断轻绳到弹簧恢复原长过程，由动量守恒可得
由能量守恒可得
联立解得
(2)取向右为正方向，M车与墙碰后到M车速度为0过程中
由能量守恒可得
联立解得
(3)小车第一次与墙相撞后向左所走路程为s1，由动能定理得
得
代入数据可得
接着小车和铁块以共同速度v2与墙第二次相碰，以向右为正方向，由动量守恒定律得
得
第二次相撞后平板车向左走的路程为s2，则有
则有
即
以后每次相碰反弹向左行的路程均以
比例减少，小车所走的路程为一个无穷等比数列之和，公式为
联立得
代入数据可得
练习册系列答案
相关题目
