题目内容
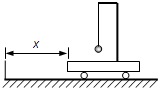 小车上有一个固定支架,支架上用长为L的绝缘细线悬挂质量为m、电量为q的小球,处于水平方向的匀强电场中.小车在距离矮墙x处,向着矮墙从静止开始做加速度为a的匀加速运动,此时,细线刚好竖直,如图所示.当小车碰到矮墙时,立即停止运动,且电场立刻消失.已知细线最大承受拉力为7mg.
小车上有一个固定支架,支架上用长为L的绝缘细线悬挂质量为m、电量为q的小球,处于水平方向的匀强电场中.小车在距离矮墙x处,向着矮墙从静止开始做加速度为a的匀加速运动,此时,细线刚好竖直,如图所示.当小车碰到矮墙时,立即停止运动,且电场立刻消失.已知细线最大承受拉力为7mg.(1)求匀强电场的电场强度;
(2)若小球能通过最高点,写出最高点时细线的拉力与x的关系式;
(3)若要使细线不断裂也不松弛,确定x的取值范围.
分析:(1)以小球为研究对象,根据运动情况,可利用牛顿第二定律和电场力公式求出场强.
(2)小球在小车静止后,做圆周运动,利用机械能守恒和圆周运动的知识求解最高点拉力和x的关系式.
(3)利用上式的结论,分析确定x的取值范围.
(2)小球在小车静止后,做圆周运动,利用机械能守恒和圆周运动的知识求解最高点拉力和x的关系式.
(3)利用上式的结论,分析确定x的取值范围.
解答:解:(1)以小球为研究对象,由于小车向左加速运动时,细线竖直,所以电场力为合外力,设匀强电场场强为E,
据牛顿第二定律得:Eq=ma
所以E=
(2)设小车与墙碰撞时车的速度为v,
由运动学公式得:v=
…①
当小车静止后,小球由于惯性,小球以绳长为半径,做圆周运动,且运动过程中机械能守恒.
设小球在最高点时绳子的拉力为F,速率为V1,
在最高点时,由牛顿第二定律得:F+mg=
…②
小球由最低点到最高点,由机械能守恒得:
mv2=2mgL+
m
…③
联立①②③解之得:T=
.?x-5mg
(3)由题境知,细线最大承受拉力为7mg.
所以x的最大值为:xmax=
×L=
当T=0时,小球恰好能到达最高点,保证绳子不松弛
所以x 的最小值为:xmin=
×L=
所以要使细线不断裂也不松弛,
≤x≤
.
答:(1)求匀强电场的电场强度
;
(2)若小球能通过最高点,写出最高点时细线的拉力与x的关系式T=
.?x-5mg;
(3)若要使细线不断裂也不松弛,确定x的取值范围为
≤x≤
.
据牛顿第二定律得:Eq=ma
所以E=
| ma |
| q |
(2)设小车与墙碰撞时车的速度为v,
由运动学公式得:v=
| 2ax |
当小车静止后,小球由于惯性,小球以绳长为半径,做圆周运动,且运动过程中机械能守恒.
设小球在最高点时绳子的拉力为F,速率为V1,
在最高点时,由牛顿第二定律得:F+mg=
m
| ||
| L |
小球由最低点到最高点,由机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 1 |
联立①②③解之得:T=
| 2ma |
| L |
(3)由题境知,细线最大承受拉力为7mg.
所以x的最大值为:xmax=
| T +5mg |
| 2ma |
| 6g |
| a |
当T=0时,小球恰好能到达最高点,保证绳子不松弛
所以x 的最小值为:xmin=
| T +5mg |
| 2ma |
| 5g |
| 2a |
所以要使细线不断裂也不松弛,
| 5g |
| 2a |
| 6g |
| a |
答:(1)求匀强电场的电场强度
| ma |
| q |
(2)若小球能通过最高点,写出最高点时细线的拉力与x的关系式T=
| 2ma |
| L |
(3)若要使细线不断裂也不松弛,确定x的取值范围为
| 5g |
| 2a |
| 6g |
| a |
点评:本题的关键是能分析出小球的运动和运动过程中遵循的规律,灵活应用机械能守恒和牛顿运动定律求解;小球绳模型在最高点的条件.

练习册系列答案
相关题目
 如图所示,小车上有一个固定支架.芰架上用长为L的细线拴住一个可视为质点的小球,小车与球一直以速度v0沿水平向左做匀速运动,已知
如图所示,小车上有一个固定支架.芰架上用长为L的细线拴住一个可视为质点的小球,小车与球一直以速度v0沿水平向左做匀速运动,已知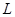 的绝缘细线悬挂质量为m、电量为q的小球,处于水平方向的匀强电场中。小车在距离矮墙x处,向着矮墙从静止开始做加速度a匀加速运动,此时,细线刚好竖直,如图所示。当小车碰到矮墙时,立即停止运动,且电场立刻消失。已知细线最大承受拉力为7mg。
的绝缘细线悬挂质量为m、电量为q的小球,处于水平方向的匀强电场中。小车在距离矮墙x处,向着矮墙从静止开始做加速度a匀加速运动,此时,细线刚好竖直,如图所示。当小车碰到矮墙时,立即停止运动,且电场立刻消失。已知细线最大承受拉力为7mg。
 <v<
<v< ,g为当地的重力加速度.当小车突然碰到与其等高的矮墙后,小车立即停止运动,则在线未被拉断的情况下,小球升高的最大高度为( )
,g为当地的重力加速度.当小车突然碰到与其等高的矮墙后,小车立即停止运动,则在线未被拉断的情况下,小球升高的最大高度为( )



 <v<
<v< ,g为当地的重力加速度.当小车突然碰到与其等高的矮墙后,小车立即停止运动,则在线未被拉断的情况下,小球升高的最大高度为( )
,g为当地的重力加速度.当小车突然碰到与其等高的矮墙后,小车立即停止运动,则在线未被拉断的情况下,小球升高的最大高度为( )


