Question

(16分)小车上有一个固定支架，支架上用长为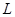的绝缘细线悬挂质量为m、电量为q的小球，处于水平方向的匀强电场中。小车在距离矮墙x处，向着矮墙从静止开始做加速度a匀加速运动，此时，细线刚好竖直，如图所示。当小车碰到矮墙时，立即停止运动，且电场立刻消失。已知细线最大承受拉力为7mg。

⑴求匀强电场的电场强度；

⑵若小球能通过最高点，写出最高点时细线的拉力与x的关系式；

⑶若要使细线不断裂也不松弛，确定x的取值范围。

 

Answer 1

【答案】

 ⑴E＝；⑵T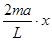＝－5mg；⑶x≤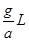或≤x≤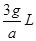

【解析】

试题分析：⑴对小球受重力mg、细线的拉力T和电场力qE作用，根据牛顿第二定律可知qE＝ma

解得匀强电场的电场强度为：E＝

⑵根据匀变速直线运动规律可知，当小车碰到矮墙瞬间小球的速度为：v₁＝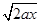

小车停止运动后，小球受mg、细线的拉力T作用，在竖直平面内做圆周运动，此时只有重力mg做功，根据动能定理有：－2mgL＝－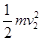

在小球运动至圆轨迹最高点时，根据牛顿第二定律和向心力公式有：T＋mg＝

联立以上各式解得：T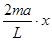＝－5mg

⑶若小球仅在下半圆周内摆动，则：mgL≥

解得：x≤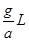

此情况中，在最低点有：T－mg＝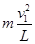

解得：T＝3mg＜7mg，符合题意要求

若小球完成完整的圆周运动，则：T₂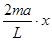＝－5mg≥0

且：T₁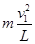＝＋mg≤7mg

联立以上各式解得：≤x≤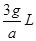

所以要使细线不断裂也不松弛， x的取值范围为：x≤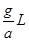或≤x≤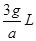

考点：本题主要考查了匀变速直线运动规律、圆周运动向心力公式、牛顿第二定律、动能定理的应用以及临界情况的分析能力问题，属于中档偏高题。