题目内容
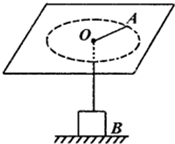 如图所示,在光滑的水平桌面上有一光滑小孔0,一根轻绳穿过小孔,一端连接质量为m=1kg的小球A,另一端连接质量为M=4kg的重物B.求:
如图所示,在光滑的水平桌面上有一光滑小孔0,一根轻绳穿过小孔,一端连接质量为m=1kg的小球A,另一端连接质量为M=4kg的重物B.求:(1)当A球沿半径为R=0.1m的圆做匀速圆周运动,其角速度为ω=10rad/s时,B对地面的压力是多少?
(2)要使B物体对地面恰好无压力,A球的角速度应为多大?(g取10m/s2)
分析:(1)对A,绳子的拉力提供A所需的向心力,根据向心力公式T=mω2r,求出绳子上拉力.B受到重力、支持力和拉力,根据B处于平衡状态,求出地面给B的支持力,根据牛顿第三定律可知物体B对地面的压力.
(2)B物体处于将要离开而尚未离开地面的临界状态时地面给它的支持力为零,由此可以求出绳子上拉力,然后以A为研究对象根据向心力公式T=mω2r可以求出A球的角速度的大小.
(2)B物体处于将要离开而尚未离开地面的临界状态时地面给它的支持力为零,由此可以求出绳子上拉力,然后以A为研究对象根据向心力公式T=mω2r可以求出A球的角速度的大小.
解答:解:(1)对小球A来说,小球受到的重力和支持力平衡.因此绳子的拉力提供向心力,则:
FT=mRω2=1×0.1×102N=10N,
对物体B来说,物体受到三个力的作用:重力Mg、绳子的拉力FT、地面的支持力FN,由力的平衡条件可得:
FT+FN=Mg 故 FN=Mg-FT
将FT=10N代入可得:FN=(4×10-10)N=30N
由牛顿第三定律可知,B对地面的压力为30 N,方向竖直向下.
(2)当B对地面恰好无压力时,有:Mg=FT′,
拉力 FT′提供小球A所需向心力,则:FT′=mRω′2
则有:ω′2=
=
rad/s=20rad/s
即:当B对地面恰好无压力时,A小球的角速度值应为20rad/s.
答:(1)当A球沿半径为R=0.1m的圆做匀速圆周运动,其角速度为ω=10rad/s时,B对地面的压力是30N,方向竖直向下
(2)要使B物体对地面恰好无压力,A球的角速度应为20rad/s.
FT=mRω2=1×0.1×102N=10N,
对物体B来说,物体受到三个力的作用:重力Mg、绳子的拉力FT、地面的支持力FN,由力的平衡条件可得:
FT+FN=Mg 故 FN=Mg-FT
将FT=10N代入可得:FN=(4×10-10)N=30N
由牛顿第三定律可知,B对地面的压力为30 N,方向竖直向下.
(2)当B对地面恰好无压力时,有:Mg=FT′,
拉力 FT′提供小球A所需向心力,则:FT′=mRω′2
则有:ω′2=
|
|
即:当B对地面恰好无压力时,A小球的角速度值应为20rad/s.
答:(1)当A球沿半径为R=0.1m的圆做匀速圆周运动,其角速度为ω=10rad/s时,B对地面的压力是30N,方向竖直向下
(2)要使B物体对地面恰好无压力,A球的角速度应为20rad/s.
点评:解决本题的关键知道绳子的拉力提供A做圆周运动的向心力,结合B受力分析列出受力平衡方程进行求解,注意研究对象的灵活选择.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别挂上小球C和物体B,在B的下端再挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时圆周运动的半径为R,现剪断连接A、B的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( ) 如图所示,在光滑的水平板的中央有一光滑的小孔,一根不可伸长的轻绳穿过小孔.绳的两端分别拴有一小球C和一质量为m的物体B,在物体B的下端还悬挂有一质量为3m的物体A.使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动的半径为R.现剪断连接A、B的绳子,稳定后,小球以2R的半径在水平面上做匀速圆周运动,则下列说法正确的( )
如图所示,在光滑的水平板的中央有一光滑的小孔,一根不可伸长的轻绳穿过小孔.绳的两端分别拴有一小球C和一质量为m的物体B,在物体B的下端还悬挂有一质量为3m的物体A.使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动的半径为R.现剪断连接A、B的绳子,稳定后,小球以2R的半径在水平面上做匀速圆周运动,则下列说法正确的( ) 如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
如图所示,在光滑的水平板的中央有一光滑的小孔,用不可伸长的轻绳穿过小孔,绳的两端分别栓上一小球C和一物体B,在B的下端再悬挂一重物A,现使小球C在水平板上以小孔为圆心做匀速圆周运动,稳定时,圆周运动半径为R.现剪断连接AB的绳子,稳定后,小球以另一半径在水平面上做匀速圆周运动,则下列说法正确的是( )
