题目内容
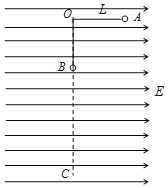
【题目】空间存在范围足够大的水平方向匀强电场，长为L的绝缘细线一端固定于O点，另一端系一带电量为正q质量为m的小球，已知电场强度
，OA处于水平方向，OC在竖直方向。小球从A点由静止释放，当小球运动到O点正下方B时细线恰好断裂
取
，
。求：
小球到达B点时的速度大小及此时细线断裂前
对小球拉力的大小；
小球从A点运动到B点过程中的最大速率；
当小球再次运动到OC线上的D点图中未标出时，小球速度的大小和方向。
【答案】
，
；
；
，方向：与竖直方向夹角为：
。
【解析】
小球由A到B过程，应用动能定理可以求出小球到达B点的速度，在B点对小球应用牛顿第二定律可以求出细线的拉力。重力与电场力的合力方向为小球的等效平衡位置，小球到达等效平衡位置时速度最大，应用动能定理可以求出小球的最大速度。绳子断裂后，小球在水平方向做匀减速直线运动，在竖直方向做自由落体运动，应用运动的合成与分解及运动学公式求出小球到达D点时的速度。
设小球运动到B点时速度大小为
，小球从A到B过程，
由动能定理得：
，
解得：
，
在B点，由牛顿第二定律得：
，
解得：
；
因为电场力与重力的合力方向与竖直方向成
，所以当小球运动到细线与竖直方向成时速率最大。
由动能定理得：
，
解得：
；
细线断裂后，小球水平方向作匀减速运动，竖直方向作自由落体运动。
水平方向加速度：
，
小球再次运动到OC线上的D点所需时间：
，
小球到D点时竖直方向的速度：
，
水平方向的速度：
，
小球的速度：
，
设小球的速度方向与竖直方向成
角，则：
，
，
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
