题目内容
(10分)如图所示，半径为R的
光滑圆弧轨道竖直放置，底端与光滑的水平轨道相接，质量为m的小球B静止光滑水平轨道上，其左侧连接了一轻质弹簧，质量为m的小球A自圆弧轨道的顶端由静止释放，重力加速度为g，小球可视为质点．
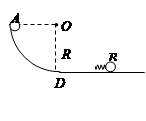
求：（1）小球A滑到圆弧面底端时的速度大小．
（2）小球A撞击轻质弹簧的过程中，弹簧的最大弹性势能为多少．
（1）
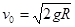（2）
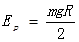
解析试题分析：（1）设A球到达圆弧底端时的速度为v0，由机械能守恒定律有：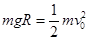 
①（2分）
A球到达圆弧底端时的速度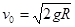 ②（2分）
（2）当A、B两球速度相同时，弹簧的弹性势能最大，设共同速度为v（1分）
由动量守恒定律有：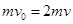 
③（2分）
得
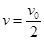④（1分）
由能量守恒可知，弹簧的最大弹性势能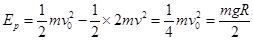
⑤（2分）
考点：机械能守恒定律 动量守恒定律
阅读快车系列答案关于机械能守恒的叙述，下列说法正确的是（ ）
| A．物体做匀速直线运动，机械能一定守恒 |
| B．物体所受合力做功为零，机械能一定守恒 |
| C．物体所受合力为零，机械能一定守恒 |
| D．物体所受的合力不等于零，机械能可能守恒 |
某人在高h处抛出一个质量为m 的物体，不计空气阻力，物体落地时速度为v，该人对物体所做的功为
A． －mgh | B． | C．mgh + | D．Mgh |
NBA篮球赛非常精彩，吸引了众多观众。经常有这样的场面：在临终场0.1s的时候，运动员把球投出且准确命中，获得比赛的胜利。如果运动员投篮过程中对篮球做功为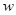
，出手高度为h1，篮筐距地面高度为h2，篮球的质量为
，空气阻力不计，则篮球进筐时的动能为
| A．W＋mgh1－mgh2 | B．W＋mgh2－mgh1 |
| C．mgh1＋mgh2－W | D．mgh2－mgh1－W |
如图所示，运动员把质量为m的足球从水平地面踢出，足球在空中达到的最高点高度为h，在最高点时的速度为v。不计空气阻力，重力加速度为g。下列说法正确的是
A．运动员踢球时对足球做功 |
B．足球上升过程克服重力做功 |
C．运动员踢球时对足球做功 |
| D．足球上升过程克服重力做功 |
如图甲所示，质量不计的弹簧竖直固定在水平面上，t＝0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球落到弹簧上压缩弹簧到最低点，然后又被弹起离开弹簧，上升到一定高度后再下落，如此反复．通过安装在弹簧下端的压力传感器，测出这一过程弹簧弹力F随时间t变化的图象如图乙所示，则( )
| A．t1时刻小球动能最大 |
| B．t2时刻小球动能最大 |
| C．t2～t3这段时间内，小球的动能先增加后减少 |
| D．t2～t3这段时间内，小球增加的动能等于弹簧减少的弹性势能 |
