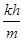题目内容
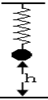
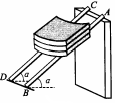
分如图所示,质量m的小物体,从光滑曲面上高度H处释放,到达底端时水平进入轴心距离L的水平传送带,传送带可由一电机驱使顺时针转动。已知物体与传送带间的动摩擦因数为μ。求:

⑴求物体到达曲面底端时的速度大小v0?
⑵若电机不开启,传送带不动,物体能够从传送带右端滑出,则物体滑离传送带右端的速度大小v1为多少?
⑶若开启电机,传送带以速率v2(v2>v0)顺时针转动,且已知物体到达传送带右端前速度已达到v2,则传送一个物体电动机对传送带多做的功为多少?

⑴求物体到达曲面底端时的速度大小v0?
⑵若电机不开启,传送带不动,物体能够从传送带右端滑出,则物体滑离传送带右端的速度大小v1为多少?
⑶若开启电机,传送带以速率v2(v2>v0)顺时针转动,且已知物体到达传送带右端前速度已达到v2,则传送一个物体电动机对传送带多做的功为多少?
⑴v0=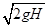 ;⑵v1=
;⑵v1= ;⑶
;⑶
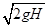 ;⑵v1=
;⑵v1= ;⑶
;⑶试题分析:⑴物体在曲面上下滑的过程中,只有重力做功,根据动能定理有:mgH=
 -0
-0解得物体到达曲面底端时的速度为:v0=
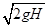 ①
①⑵物体在水平传送带上滑动时受滑动摩擦力f作用,且只有滑动摩擦力做功,有:f=μmg ②
根据动能定理有:-fL=
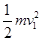 -
- ③
③由①②③式联立解得物体滑离传送带右端的速度为:v1=

⑶当开启电机,传送带以速率v2(v2>v0)顺时针转动时,物体在水平传送带上受到向右的滑动摩擦力作用而做匀加速直线运动至与传送带速度相等,后再匀速运动至右端,匀速运动阶段不受滑动摩擦力作用,设物体加速运动的加速度为a,时间为t,位移为x1,根据牛顿第二定律有:f=ma ④
根据加速度定义式有:a=
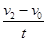 ⑤
⑤对物块根据动能定理有:fx1=
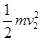 -
- ⑥
⑥皮带移动的距离为:x2=v2t ⑦
因物块在皮带上滑动产生的内能为:Q=f(x2-x1) ⑧
根据功能关系可知,传送一个物体电动机对传送带多做的功为:W=Q+
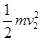 -
- ⑨
⑨由②④⑤⑥⑦⑧⑨式联立解得:W=


练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
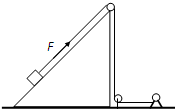

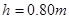 的水平桌面一端的边缘放置一个质量
的水平桌面一端的边缘放置一个质量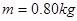 的木块
的木块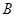 ,桌面的另一端有一块质量
,桌面的另一端有一块质量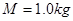 的木块
的木块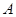 以初速度
以初速度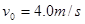 开始向着木块
开始向着木块 与
与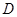 点。设两木块均可以看作质点,它们的碰撞时间极短,且已知
点。设两木块均可以看作质点,它们的碰撞时间极短,且已知 ,木块A与桌面间的动摩擦因数
,木块A与桌面间的动摩擦因数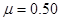 ,重力加速度取
,重力加速度取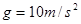 。求:
。求: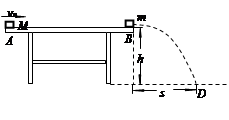
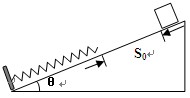
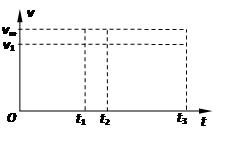 (2)若滑块在沿斜面向下运动的整个过程中最大速度大小为vm,求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W;
(2)若滑块在沿斜面向下运动的整个过程中最大速度大小为vm,求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W;