题目内容
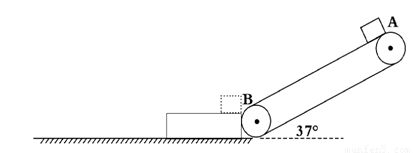
（16分）如图所示，某传送带与地面倾角θ＝37o，AB之间距离L1=2.05m，传送带以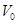
＝1.0m/s的速率逆时针转动。质量为M=1.0kg，长度L2=1.0m的木板上表面与小物块的动摩擦因数μ2＝0.4，下表面与水平地面间的动摩擦因数μ3＝0.1，开始时长木板靠近传送带B端并处于静止状态。现在传送带上端A无初速地放一个质量为ｍ＝1.0kg的小物块，它与传送带之间的动摩擦因数为μ1＝0.5，（假设物块在滑离传送带至木板右端时速率不变，sin37o＝0.6，cos37 o =0.8, g=10
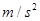）。求：
（1）物块离开B点的速度大小；
（2）物块在木板上滑过的距离；
（3）木板在地面上能滑过的最大距离。
（1）3m/s （2）0.75m （3）0.75m
【解析】
试题分析：（1）刚开始物块相对传送带往上滑其加速度为:
a1=gsin37o+μ1gcos37o=10 m/s2 …（1分）
达到传送带速度V0用的时间: t1= V0/ a1=0.1s（1分）
位移: s1=1/2 a1 t12=0.05m （1分）
过后因μ1〈tan37o 故物块相对传送带往下滑其加速度:
a2=gsin37o-μ1gcos37o=2 m/s2 …（1分）
由s2=L1-s1=(VB2-VO2)/2 a2 …（1分） VB=3m/s （1分）
(2)物块滑上木板相对滑动时做匀减速运动，其加速度:a3=-μ2g=-4 m/s2 （1分）
木板的加速度: a4=〔μ2mg-μ3 (mg+Mg)〕/M=2 m/s2, （1分）
设经过t2物块与木板达到相同速度V2，则 VB + a3 t2= a4 t2 故t2 =0.5s
V2= a4 t2 =1m/s …（1分）
物块对地位移: s3=( V22- VB2)/2 a3=1 m （1分）
木板对地位移: s4= V22/2 a4=0.25m （1分）
物块在木板上滑过的距离: △s= s3- s4=0.75m （1分）
(3)因μ3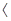
μ2物块能与木板保持相对静止，其整体加速度为:a5=-μ3g=-1m/s2, …（1分）
物块与木板做匀减速运动到停止的位移: s5= -V22/2 a5=0.5m （1分）
木板对地的位移: s板= s4 +s5=0.75m （2分）
考点：牛顿运动定律及应用
新非凡教辅冲刺100分系列答案
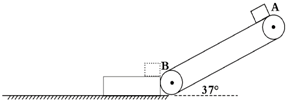如图所示，某传送带与地面倾角θ=37°，AB之间距离
＝1.0m/s的速率逆时针转动。质量为M=1.0kg，长度L2=1.0m的木板上表面与小物块的动摩擦因数μ2＝0.4，下表面与水平地面间的动摩擦因数μ3＝0.1，开始时长木板靠近传送带B端并处于静止状态。现在传送带上端A无初速地放一个质量为ｍ＝1.0kg的小物块，它与传送带之间的动摩擦因数为μ1＝0.5，（假设物块在滑离传送带至木板右端时速率不变，sin37o＝0.6，cos37 o =0.8, g=10
）。求：
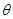=37o，传送带AB长度xo=l0m。有一水平平台CD高度保持6．45m不变。现调整D端位置，当D、B的水平距离合适时，自D端水平抛出的物体恰好从B点沿BA方向冲上斜面，此后D端固定不动，g=l0m/s2。另外，传送带B端上方安装一极短的小平面，与传送带AB平行共面，保证自下而上传送的物体能沿AB方向由B点斜向上抛出。（sin37o=0．6，cos37o=0．8）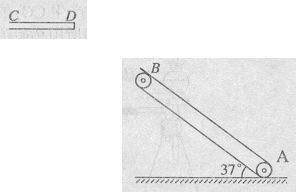
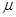1=0．9，自A点沿传送带方向以某一初速度冲上传送带时，恰能水平落到水平台的D端，求物体甲的最大初速度vo1
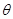=37o，传送带AB长度xo=l0m。有一水平平台CD高度保持6．45m不变。现调整D端位置，当D、B的水平距离合适时，自D端水平抛出的物体恰好从B点沿BA方向冲上斜面，此后D端固定不动，g=l0m/s2。另外，传送带B端上方安装一极短的小平面，与传送带AB平行共面，保证自下而上传送的物体能沿AB方向由B点斜向上抛出。（sin37o=0．6，cos37o=0．8）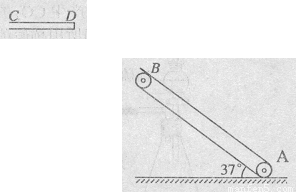
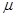1=0．9，自A点沿传送带方向以某一初速度冲上传送带时，恰能水平落到水平台的D端，求物体甲的最大初速度vo1