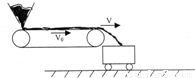
题目内容
如图所示,某传送带装置倾斜放置,倾角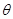 =37o,传送带AB长度xo=l0m。有一水平平台CD高度保持6.45m不变。现调整D端位置,当D、B的水平距离合适时,自D端水平抛出的物体恰好从B点沿BA方向冲上斜面,此后D端固定不动,g=l0m/s2。另外,传送带B端上方安装一极短的小平面,与传送带AB平行共面,保证自下而上传送的物体能沿AB方向由B点斜向上抛出。(sin37o=0.6,cos37o=0.8)
=37o,传送带AB长度xo=l0m。有一水平平台CD高度保持6.45m不变。现调整D端位置,当D、B的水平距离合适时,自D端水平抛出的物体恰好从B点沿BA方向冲上斜面,此后D端固定不动,g=l0m/s2。另外,传送带B端上方安装一极短的小平面,与传送带AB平行共面,保证自下而上传送的物体能沿AB方向由B点斜向上抛出。(sin37o=0.6,cos37o=0.8)
(1)求D、B的水平距离;
(2)若传送带以5m/s的速度逆时针匀速运行,某物体甲与传送带间动摩擦因数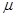 1=0.9,自A点沿传送带方向以某一初速度冲上传送带时,恰能水平落到水平台的D端,求物体甲的最大初速度vo1
1=0.9,自A点沿传送带方向以某一初速度冲上传送带时,恰能水平落到水平台的D端,求物体甲的最大初速度vo1
(3)若传送带逆时针匀速运行,某物体乙与传送带间动摩擦因数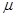 2=0.6,自A点以vo2=11m/s的初速度沿传送带方向冲上传送带时,恰能水平落到水平台的D端,求传送带的速度v′。
2=0.6,自A点以vo2=11m/s的初速度沿传送带方向冲上传送带时,恰能水平落到水平台的D端,求传送带的速度v′。
(1)1.2m(2)v01= 17m/s(3)2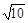 m/s
m/s
【解析】
试题分析:(1)设水平抛出物体的初速度v0,经时间t落入传送带上时,竖直分速度为vy ,竖直方向:
h - x0sinθ = 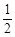 gt2
gt2
vy = gt
tanθ= 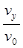
水平方向距离 x = v0t
∴ x = 1.2m(4分)
(2)由(1)中得 sinθ = 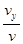 (1分)
(1分)
所以物体从传送带上落下时 v = 5m/s
则物体甲到B端的速度为v = 5m/s,则恰能水平落到水平台的D端
由动能定理得:-mg x0sinθ-μ1mgcosθx0 = 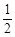 mv2-
mv2-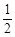 mv012(2分)
mv012(2分)
∴ v01= 17m/s(1分)
(3)若传送带对物体的摩擦力方向始终向下,设物体到B端速度v1
由动能定理得:-mg x0sinθ-μ2mgcosθx0 =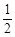 mv12-
mv12-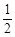 mv022
mv022
v1无解
若传送带对物体的摩擦力方向始终向上,设物体到B端速度v2
由动能定理得: -mgx0sinθ+μ2mgcosθx0 =
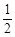 mv22-
mv22-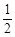 mv022
mv022
∴ v2= 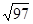 m/s >5m/s
m/s >5m/s
故只能是摩擦力方向先向下后向上(1分)
当摩擦力方向向下时,由牛顿第二定律得
mgsinθ+μ2mgcosθ = ma1(1分)
∴ a1= 10.8m/s2
当摩擦力方向向上时,由牛顿第二定律得
mgsinθ-μ2mgcosθ = ma2(1分)
∴ a2= 1.2m/s2
设传送带速度为v′,则有
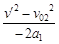 +
+ 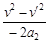 = x0(2分)
= x0(2分)
∴ v′= 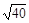 m/s = 2
m/s = 2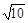 m/s(1分)
m/s(1分)
考点:考查牛顿第二定律和功能关系
点评:本题难度较小,判断摩擦力方向是本题的关键,因此需要判断物块相对于传送带的速度方向

 星级口算天天练系列答案
星级口算天天练系列答案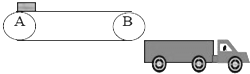 如图所示为某工厂装载货物的原理示意图,设传送AB 的长度为8m,货物与传送带的动摩擦力因数为0.6,货物以初速度10m/s滑至传送带的A 端,车厢长为12m,车厢的顶部到B 顶端的高度差为1.25m,通过调节传送带(瞬时针)的速度可合理地将车厢装满以实现自动装货,则下列说法中正确的是( )
如图所示为某工厂装载货物的原理示意图,设传送AB 的长度为8m,货物与传送带的动摩擦力因数为0.6,货物以初速度10m/s滑至传送带的A 端,车厢长为12m,车厢的顶部到B 顶端的高度差为1.25m,通过调节传送带(瞬时针)的速度可合理地将车厢装满以实现自动装货,则下列说法中正确的是( )| A、车厢到B 的水平距离至少1m 时,货物才能装进车厢 | B、若传送带逆时针转动时,货物不可能装进车厢 | C、只要传带的速度足够大,货物就可到达车厢的右端 | D、若要货物达到车厢的右端,司机需要把车向左移动一段距离 |
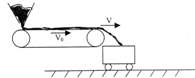 如图所示,用水平传送带向车厢装煤,传送带长L=4.5m,速度为v0=3.5m/s.煤斗送到传送带左端的煤为每秒钟m0=2.0kg,煤落到传送带上时速度忽略不计,动摩擦因数为μ=0.10,已知煤在传送带速度始终小于v0,整个装置长时间连续工作.(g=10m/s2,结果保留2位有效数字)
如图所示,用水平传送带向车厢装煤,传送带长L=4.5m,速度为v0=3.5m/s.煤斗送到传送带左端的煤为每秒钟m0=2.0kg,煤落到传送带上时速度忽略不计,动摩擦因数为μ=0.10,已知煤在传送带速度始终小于v0,整个装置长时间连续工作.(g=10m/s2,结果保留2位有效数字)