题目内容
 在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,试求小球做圆周运动的向心加速度和周期.
在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,试求小球做圆周运动的向心加速度和周期.分析:小球所受的重力和拉力的合力提供圆周运动的向心力,根据mgtanθ=ma,求出圆周运动的向心加速度;根据mgtanθ=mr(
)2,求出小球的周期.
| 2π |
| T |
解答:解:小球所受的重力和拉力的合力提供圆周运动的向心力,根据mgtanθ=ma得
a=gtanθ
由mgtanθ=mr(
)2得
做圆周运动的半径为
r=Lsinθ
联立解得
T=2π
答:小球做圆周运动的向心加速度和周期为 a=gtanθ T=2π
a=gtanθ
由mgtanθ=mr(
| 2π |
| T |
做圆周运动的半径为
r=Lsinθ
联立解得
T=2π
| Lcosθ |
答:小球做圆周运动的向心加速度和周期为 a=gtanθ T=2π
| Lcosθ |
点评:解决本题的关键知道小球所受的重力和拉力的合力提供圆周运动的向心力.小球在竖直方向上平衡,即拉力在竖直方向的分力等于重力.

练习册系列答案
相关题目
 在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,求小球做匀速圆周运动的周期.
在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,求小球做匀速圆周运动的周期. 在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,试求小球做圆周运动的周期
在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,试求小球做圆周运动的周期 在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,求:
在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,求: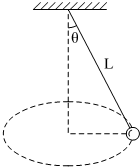 在如图所示的圆锥摆中,已知绳子长度为L=2m,绳子转动过程中与竖直方向的夹角为θ=37°,试求小球做匀速圆周运动的周期.
在如图所示的圆锥摆中,已知绳子长度为L=2m,绳子转动过程中与竖直方向的夹角为θ=37°,试求小球做匀速圆周运动的周期.