Question

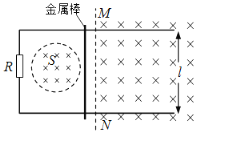
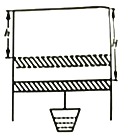
【题目】如图所示，两光滑金属导轨，间距d＝0.2m，在桌面上的部分是水平的，处在磁感应强度B＝0.1T、方向竖直向下的有界磁场中，电阻R＝3Ω，桌面高H＝0.8m，金属杆ab的质量m＝0.2kg，电阻r＝1Ω，在导轨上距桌面h＝0.2m的高处由静止释放，落地点距桌面左边缘的水平距离s＝0.4m，g＝10m/s2. 求：

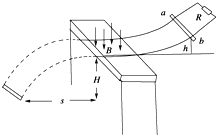
(1)金属杆进入磁场时，R上的电流大小；

(2)整个过程中R上产生的热量．

(3)整个过程中通过R的电荷量.

Answer 1

【答案】(1)0.01A ； (2) 0.225J. (3) 10C

【解析】

（1）根据动能定理求出杆子进入磁场时的速度，通过切割产生的感应电动势公式求出感应电动势的大小，结合闭合电路欧姆定律求出感应电流的大小．
（2）根据平抛运动的规律求出金属杆滑出导轨瞬间的速度；根据能量守恒定律求出整个过程中回路产生的热量，从而得出整个过程中电阻R放出的热量．

（3）根据动量定理求解整个过程中通过R的电荷量.

（1）ab棒刚进入磁场的瞬间，速率为v，由机械能守恒定律得mgh＝mv2，

此时感应电动势E＝Bdv＝0.1×0.2×2V＝0.04V

，方向：棒中由a→b.

（2）金属杆平抛初速度为v′，则有，

解得

由能量守恒，有Q＝mgh－mv′2＝(0.2×10×0.2－×0.2×12)J＝0.3J

R放出的热量.

（3）金属棒从进入磁场到出离磁场，由动量定理： 其中

带入数据解得：q=10C .