题目内容
4.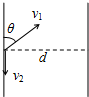 已知船在静水中的速度大小始终为v1=10m/s,当船头方向与河岸上游的夹角θ=370时,测得船经过t1=100s的航行时间恰好沿图中虚线到达河的正对岸,已知河水流速处处相等且大小为v2,河的宽度处处相同,sin37°=0.6,cos37°=0.8.求:
已知船在静水中的速度大小始终为v1=10m/s,当船头方向与河岸上游的夹角θ=370时,测得船经过t1=100s的航行时间恰好沿图中虚线到达河的正对岸,已知河水流速处处相等且大小为v2,河的宽度处处相同,sin37°=0.6,cos37°=0.8.求:(1)河水流速v2;
(2)河的宽度d;
(3)要使该船渡过此河的时间最短,船头方向应朝哪?并求最短时间t2.
分析 (1)根据运动的合成,结合三角函数,即可求解;
(2)根据速度的合成与分解,结合位移公式,即可求解;
(3)当船头方向垂直河岸时,过河时间最短,并由位移公式,可求出运动的最短时间.
解答 解:(1)小船恰好沿图中虚线到达河的正对岸,
则有v1cosθ=v2
得v2=8m/s
(2)河宽度为d=v1sinθt1,
得d=600m
(3)当船头方向垂直河岸时,过河时间最短
由${t_2}=\frac{d}{v_1}$
得t2=60s
答:(1)河水流速8m/s;
(2)河的宽度600m;
(3)要使该船渡过此河的时间最短,船头方向垂直河岸,则最短时间60s.
点评 考查运动的合成与分解,掌握运动学公式,注意分运动与合运动的同时性,注意区分时间最短与位移最短的船向.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
14.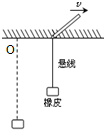 如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右拨动,一段时间内铅笔的速度v保持不变,悬线保持竖直.则关于这段时间内橡皮运动情况,下列说法中正确的是( )
如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右拨动,一段时间内铅笔的速度v保持不变,悬线保持竖直.则关于这段时间内橡皮运动情况,下列说法中正确的是( )
 如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右拨动,一段时间内铅笔的速度v保持不变,悬线保持竖直.则关于这段时间内橡皮运动情况,下列说法中正确的是( )
如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右拨动,一段时间内铅笔的速度v保持不变,悬线保持竖直.则关于这段时间内橡皮运动情况,下列说法中正确的是( )| A. | 橡皮的速度大小为v,方向水平向右 | |
| B. | 橡皮的速度大小为v,方向竖直向上 | |
| C. | 橡皮的速度大小为2 v,方向斜向右上方 | |
| D. | 橡皮的速度大小为$\sqrt{2}$v,方向斜向右上方 |
19.小球质量为2m,以速度v沿水平方向撞击竖直墙壁,以$\frac{4}{5}$v的速率反弹回来,球与墙的撞击时间为t,则在撞击过程中,球对墙的平均作用力的大小是$\frac{18mv}{5t}$.
9.在物理学理论建立的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法中正确的是( )
| A. | 安培提出了分子电流假说 | |
| B. | 卡文迪许通过实验精确测出万有引力常量 | |
| C. | 牛顿提出的万有引力定律奠定了天体力学的基础 | |
| D. | 奥斯特发现电流的磁效应 |
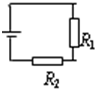 如图所示的电路中,R1是光敏电阻,R2是定值电阻,当光照加强的时候,R2两端的电压将变大(变大或变小)
如图所示的电路中,R1是光敏电阻,R2是定值电阻,当光照加强的时候,R2两端的电压将变大(变大或变小)

 如图所示,两个气缸内封有一定质量的气体,两活塞通过细杆连接,活塞截面积SB=2SA,外界大气压为1atm,当活塞平衡时,A缸内气体压强为PA=2atm,则B缸内气体压强PB为多大?(不计摩擦)
如图所示,两个气缸内封有一定质量的气体,两活塞通过细杆连接,活塞截面积SB=2SA,外界大气压为1atm,当活塞平衡时,A缸内气体压强为PA=2atm,则B缸内气体压强PB为多大?(不计摩擦) 如图所示,在一静止小车上有一水平横杆AB,可绕过中点O的水平轴无摩擦转动,A端用细绳挂一重物,B端用一竖直轻弹簧连于车上,当重物在水平向左的恒力F作用下被向左拉起后,与原来相比悬挂重物的细绳张力大小将变大,弹簧的伸长量将不变.(填变大,变小或不变)
如图所示,在一静止小车上有一水平横杆AB,可绕过中点O的水平轴无摩擦转动,A端用细绳挂一重物,B端用一竖直轻弹簧连于车上,当重物在水平向左的恒力F作用下被向左拉起后,与原来相比悬挂重物的细绳张力大小将变大,弹簧的伸长量将不变.(填变大,变小或不变)