题目内容
19.小球质量为2m,以速度v沿水平方向撞击竖直墙壁,以$\frac{4}{5}$v的速率反弹回来,球与墙的撞击时间为t,则在撞击过程中,球对墙的平均作用力的大小是$\frac{18mv}{5t}$.分析 根据动量定理,合外力的冲量等于小球动量的变化量,墙对小球的平均作用力,根据牛顿第三定律即可求得球对墙的平均作用力.
解答 解:规定以初速度方向为正,根据动量定理得:
$\overline{F}t=-0.8v•2m-2mv$
解得:$\overline{F}=\frac{18mv}{5t}$
跟据牛顿第三定律可知球对墙的平均作用力为$\frac{18mv}{5t}$.
故答案为:$\frac{18mv}{5t}$
点评 本题主要考查了动量定理的直接应用,对于矢量的加减,我们要考虑方向,应该规定正方向.

练习册系列答案
相关题目
10.物体在合力作用下做直线运动的v-t图象如图所示.下列表述正确的是( )
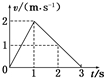

| A. | 在0~1s内,合力做正功 | B. | 在0~2s内,合力总是做负功 | ||
| C. | 在1s~2s内,合力不做功 | D. | 在0~3s内,合力总是做正功 |
14.下列说法中正确的是( )
| A. | 汤姆生通过研究阴极射线实验,发现了电子和质子的存在 | |
| B. | 裂变物质体积小于临界体积时,链式反应不能进行 | |
| C. | 卢瑟福的α粒子散射实验证明了原子核是由质子和中子组成的 | |
| D. | 衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚形成的 |
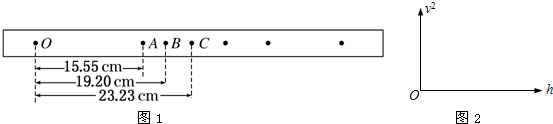
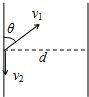 已知船在静水中的速度大小始终为v1=10m/s,当船头方向与河岸上游的夹角θ=370时,测得船经过t1=100s的航行时间恰好沿图中虚线到达河的正对岸,已知河水流速处处相等且大小为v2,河的宽度处处相同,sin37°=0.6,cos37°=0.8.求:
已知船在静水中的速度大小始终为v1=10m/s,当船头方向与河岸上游的夹角θ=370时,测得船经过t1=100s的航行时间恰好沿图中虚线到达河的正对岸,已知河水流速处处相等且大小为v2,河的宽度处处相同,sin37°=0.6,cos37°=0.8.求: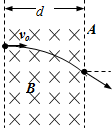 如图所示,一个电子以速度v0垂直射入磁感应强度为B,宽为d的匀强磁场中,穿出磁场的速度方向与电子原来的入射方向的夹角为30°,(电子重力忽略不计)求:
如图所示,一个电子以速度v0垂直射入磁感应强度为B,宽为d的匀强磁场中,穿出磁场的速度方向与电子原来的入射方向的夹角为30°,(电子重力忽略不计)求: 为了利用海洋资源,海洋工作者有时根据水流切割地磁场所产生的感 应电动势来测量海水的流速.假设海洋某处的地磁场竖直分量为B=0.5×10-4T,水流是南北流向,如图将两个电极竖直插入此处海水中,且保持两电极的连线垂直水流方向.若两极相距L=10m,与两电极相连的灵敏电压表的读数为U=2mV,则海水的流速大小为4m/s.
为了利用海洋资源,海洋工作者有时根据水流切割地磁场所产生的感 应电动势来测量海水的流速.假设海洋某处的地磁场竖直分量为B=0.5×10-4T,水流是南北流向,如图将两个电极竖直插入此处海水中,且保持两电极的连线垂直水流方向.若两极相距L=10m,与两电极相连的灵敏电压表的读数为U=2mV,则海水的流速大小为4m/s.