题目内容
15.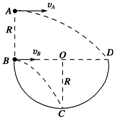 如图所示,BOD是半圆的水平直径,OC为竖直半径,半圆半径为R,A在B点正上方高R处,现有两相同小球分别从A、B两点以一定初速度水平抛出,分别击中半圆上的D点和C点,已知B球击中C点时动能为Ek,不计空气阻力,则A球击中D点时动能为( )
如图所示,BOD是半圆的水平直径,OC为竖直半径,半圆半径为R,A在B点正上方高R处,现有两相同小球分别从A、B两点以一定初速度水平抛出,分别击中半圆上的D点和C点,已知B球击中C点时动能为Ek,不计空气阻力,则A球击中D点时动能为( )| A. | 2Ek | B. | $\frac{8}{5}$Ek | C. | $\frac{5}{4}$Ek | D. | $\sqrt{5}$Ek |
分析 两个小球都做平抛运动,根据平抛运动的基本公式求出初速度,再分别对两球的运动过程,应用动能定理列式求解.
解答 解:两个小球都做平抛运动,下落的高度相同都是R,根据R=$\frac{1}{2}g{t}^{2}$可知,运动的时间为:t=$\sqrt{\frac{2R}{g}}$,
根据图象可知,A球运动的水平位移为2R,则A球的初速度为:${v}_{A}=\frac{2R}{t}=\sqrt{2gR}$,
B球的水平位移为R,则B球的初速度为:${v}_{B}=\frac{R}{t}=\sqrt{\frac{1}{2}gR}$,
A球从A到D的过程中,根据动能定理得:${E}_{kD}=mgR+\frac{1}{2}m{{v}_{A}}^{2}=2mgR$…①,
B球从B到C的过程中,根据动能定理得:${E}_{k}=mgR+\frac{1}{2}m{{v}_{B}}^{2}=\frac{5}{4}mgR$…②,
由①②得:${E}_{kD}=\frac{8}{5}{E}_{k}$,故B正确.
故选:B
点评 本题主要考查了动能定理以及平抛运动基本公式的直接应用,解题的关键是要能根据图象得出两个小球下落的高度和水平位移,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.某行星的卫星,在靠近行星表面的轨道上运行,已知引力常量G,若要计算该行星的密度,唯一要测出的物理量是( )
| A. | 行星的半径 | B. | 卫星的半径 | ||
| C. | 卫星的线速度 | D. | 卫星绕行星运动的周期 |
10.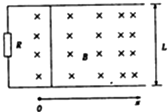 如图,两根电阻不计的平行光滑金属导轨水平放置,一端与电阻相连,导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T,一根金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=4m/s沿导轨向右运动,运动过程中电阻消耗的功率不变.则( )
如图,两根电阻不计的平行光滑金属导轨水平放置,一端与电阻相连,导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T,一根金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=4m/s沿导轨向右运动,运动过程中电阻消耗的功率不变.则( )
 如图,两根电阻不计的平行光滑金属导轨水平放置,一端与电阻相连,导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T,一根金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=4m/s沿导轨向右运动,运动过程中电阻消耗的功率不变.则( )
如图,两根电阻不计的平行光滑金属导轨水平放置,一端与电阻相连,导轨x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T,一根金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=4m/s沿导轨向右运动,运动过程中电阻消耗的功率不变.则( )| A. | 金属棒在运动过程中产生的电动势不变 | |
| B. | 金属棒在运动过程中产生的安培力大小不变 | |
| C. | 金属棒在x=3m处的速度为2m/s | |
| D. | 金属棒在x=3m处的速度为1m/s |
10.可视为点电荷的A、B两带电小球固定在真空中,所带电荷量均为q,若仅将A球所带电荷量变为-q,则B球所受的库仑力( )
| A. | 大小和方向均不变 | B. | 大小和方向均改变 | ||
| C. | 大小不变、方向改变 | D. | 大小改变、方向不变 |

 一艘小船从河岸的A处出发渡河,小船保持与河岸垂直方向行驶,经过10min到达正对岸下游120m的C处,如图所示.如果小船保持原来的速度大小不变逆水斜向上游与河岸成α角方向行驶,则经过12.5min恰好到达正对岸的B处,求:
一艘小船从河岸的A处出发渡河,小船保持与河岸垂直方向行驶,经过10min到达正对岸下游120m的C处,如图所示.如果小船保持原来的速度大小不变逆水斜向上游与河岸成α角方向行驶,则经过12.5min恰好到达正对岸的B处,求: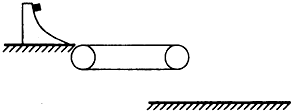 如图所示,传送带水平部分长为1m,以v0=4m/s的速度沿顺时针方向匀速转动,先将一质量为m的物体从光滑曲面由静止释放,滑到底端后水平自然进入传送带部分,并从传送带右端滑出.已知传送带上表面离地面的高度为1.25m,物体与传送带间的动摩擦因数μ=0.4,物体从曲面上释放的点离传送带的高度为h.求:
如图所示,传送带水平部分长为1m,以v0=4m/s的速度沿顺时针方向匀速转动,先将一质量为m的物体从光滑曲面由静止释放,滑到底端后水平自然进入传送带部分,并从传送带右端滑出.已知传送带上表面离地面的高度为1.25m,物体与传送带间的动摩擦因数μ=0.4,物体从曲面上释放的点离传送带的高度为h.求: