题目内容
7.万有引力定律清楚的向人们揭示复杂运动的背后隐藏着简洁的科学规律,天上和地上的万物遵循同样的科学法则.(1)当卡文迪许测量出引力常数G以后,他骄傲地说自己是“称量出地球质量”的人.当时已知地面的重力加速度g和地球半径R,根据以上条件,求地球的质量;
(2)随着我国“嫦娥三号”探测器降落月球,“玉兔”巡视器对月球进行探索,我国对月球的了解越来越深入.若已知月球半径为R月,月球表面的重力加速度为g月,嫦娥三号在降落月球前某阶段绕月球做匀速圆周运动的周期为T,试求嫦娥三号该阶段绕月球运动的轨道半径.
分析 (1)根据地球表面的物体受到的重力等于万有引力$\frac{GMm}{{R}^{2}}$=mg,可解得地球的质量M.
(2)根据月球表面的物体受到的重力等于万有引力列式,嫦娥三号在降落月球前某阶段绕月球做匀速圆周运动,根据万有引力提供向心力列式,联立方程即可求解.
解答 解:(1)设地球的质量为M,某物体的质量为m,则根据地球对物体的吸引力就是物体的重力可知:mg=$\frac{GMm}{R^2}$,
解得地球的质量为:M=$\frac{{g{R^2}}}{G}$;
(2)因为月球表面的重力加速度为g月,故有:mg月=$\frac{{G{M_月}m}}{{{R_月}^2}}$,
嫦娥三号在降落月球前某阶段绕月球做匀速圆周运动,则有:$\frac{{G{M_月}{m_星}}}{r^2}$=${m_星}\frac{{4{π^2}r}}{T^2}$,
联立以上两式,解之得:嫦娥三号该阶段绕月球运动的轨道半径为:r=$\root{3}{{\frac{{{g_月}{T^2}{R_月}^2}}{{4{π^2}}}}}$.
答:(1)地球的质量为$\frac{g{R}^{2}}{G}$;
(2)嫦娥三号该阶段绕月球运动的轨道半径为$\root{3}{\frac{{g}_{月}{T}^{2}{{R}_{月}}^{2}}{4{π}^{2}}}$.
点评 本题要掌握两个关系:星球表面的物体受到的重力等于万有引力;环绕天体绕中心天体做圆周运动所需要的向心力由万有引力提供.这两个关系可以解决天体运动的一切问题.

练习册系列答案
相关题目
17.关于花粉悬浮在水中做布朗运动的下列说法中,正确的是( )
| A. | 布朗运动就是水分子的运动 | |
| B. | 布朗运动是水分子无规则运动的反映 | |
| C. | 温度越低时,布朗运动越明显 | |
| D. | 花粉颗粒越大,由于同时跟它撞击的水分子数目越多,因而布朗运动也就激烈 |
18.从同一高度落下的玻璃杯,掉在水泥地面上易碎,而掉在软垫上不易碎,这是因为玻璃杯跟水泥地面相碰时( )
| A. | 受到的冲量较大 | B. | 碰撞时间较长 | ||
| C. | 动量改变较大 | D. | 碰撞时受到的冲力较大 |
15.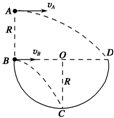 如图所示,BOD是半圆的水平直径,OC为竖直半径,半圆半径为R,A在B点正上方高R处,现有两相同小球分别从A、B两点以一定初速度水平抛出,分别击中半圆上的D点和C点,已知B球击中C点时动能为Ek,不计空气阻力,则A球击中D点时动能为( )
如图所示,BOD是半圆的水平直径,OC为竖直半径,半圆半径为R,A在B点正上方高R处,现有两相同小球分别从A、B两点以一定初速度水平抛出,分别击中半圆上的D点和C点,已知B球击中C点时动能为Ek,不计空气阻力,则A球击中D点时动能为( )
 如图所示,BOD是半圆的水平直径,OC为竖直半径,半圆半径为R,A在B点正上方高R处,现有两相同小球分别从A、B两点以一定初速度水平抛出,分别击中半圆上的D点和C点,已知B球击中C点时动能为Ek,不计空气阻力,则A球击中D点时动能为( )
如图所示,BOD是半圆的水平直径,OC为竖直半径,半圆半径为R,A在B点正上方高R处,现有两相同小球分别从A、B两点以一定初速度水平抛出,分别击中半圆上的D点和C点,已知B球击中C点时动能为Ek,不计空气阻力,则A球击中D点时动能为( )| A. | 2Ek | B. | $\frac{8}{5}$Ek | C. | $\frac{5}{4}$Ek | D. | $\sqrt{5}$Ek |
2.某点电荷和金属圆环间的电场线分布如图所示.下列说法正确的是( )


| A. | b点的电势低于a点的电势 | |
| B. | 若将一正试探电荷由a点移到b点,电场力做负功 | |
| C. | c点的电场强度与d点的电场强度大小无法判断 | |
| D. | 若将一正试探电荷从d点由静止释放,电荷将沿着电场线由d到c |
12. (多选)如图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB、水平的起跳平台BC和着陆雪道CD组成,AB与BC平滑连接.运动员从助滑雪道AB上由静止开始在重力作用下下滑,滑到C点后水平飞出,落到CD上的F点.E是运动轨迹上的某一点,在该点运动员的速度方向与轨道CD平行,E′点是E点在斜面上的垂直投影.设运动员从C到E与从E到F的运动时间分别为tCE和tEF.不计飞行中的空气阻力,下面说法或结论正确的是( )
(多选)如图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB、水平的起跳平台BC和着陆雪道CD组成,AB与BC平滑连接.运动员从助滑雪道AB上由静止开始在重力作用下下滑,滑到C点后水平飞出,落到CD上的F点.E是运动轨迹上的某一点,在该点运动员的速度方向与轨道CD平行,E′点是E点在斜面上的垂直投影.设运动员从C到E与从E到F的运动时间分别为tCE和tEF.不计飞行中的空气阻力,下面说法或结论正确的是( )
 (多选)如图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB、水平的起跳平台BC和着陆雪道CD组成,AB与BC平滑连接.运动员从助滑雪道AB上由静止开始在重力作用下下滑,滑到C点后水平飞出,落到CD上的F点.E是运动轨迹上的某一点,在该点运动员的速度方向与轨道CD平行,E′点是E点在斜面上的垂直投影.设运动员从C到E与从E到F的运动时间分别为tCE和tEF.不计飞行中的空气阻力,下面说法或结论正确的是( )
(多选)如图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB、水平的起跳平台BC和着陆雪道CD组成,AB与BC平滑连接.运动员从助滑雪道AB上由静止开始在重力作用下下滑,滑到C点后水平飞出,落到CD上的F点.E是运动轨迹上的某一点,在该点运动员的速度方向与轨道CD平行,E′点是E点在斜面上的垂直投影.设运动员从C到E与从E到F的运动时间分别为tCE和tEF.不计飞行中的空气阻力,下面说法或结论正确的是( )| A. | 运动员在F点的速度方向与从C点飞出时的速度大小无关 | |
| B. | tCE:tEF=1:2 | |
| C. | CE′:E′F可能等于1:3 | |
| D. | CE′:E′F可能等于1:2 |
19.关于能的转化和守恒以下结论正确的是( )
| A. | 功可以全部转化为热,而热不能全部转化为功 | |
| B. | 满足能量守恒定律的物理过程都能自发进行 | |
| C. | 任何条件下,热量都不会由低温物体转移到高温物体 | |
| D. | 物体的动能和势能可以相互转化 |
 如图为一架简易的投石机示意图,该装置由一根一端开口长为x0的光滑硬质塑料管和固定于另一端的轻弹簧组成,并通过铰链固定于木架上.不用时弹簧自由端恰与管口齐平;现在弹簧上端放置一质量为m的光滑小钢珠,当将管子向右转动到与竖直面成60°的位置时,弹簧长度变为$\frac{3}{4}$x0.此时快速向左拨动管子,钢珠恰好在管子竖直时从管口飞出,并垂直击中正前方的目标靶靶心.已知目标靶靶心离竖直杆顶的水平距离为L,竖直距离为$\frac{L}{2}$,试分析:
如图为一架简易的投石机示意图,该装置由一根一端开口长为x0的光滑硬质塑料管和固定于另一端的轻弹簧组成,并通过铰链固定于木架上.不用时弹簧自由端恰与管口齐平;现在弹簧上端放置一质量为m的光滑小钢珠,当将管子向右转动到与竖直面成60°的位置时,弹簧长度变为$\frac{3}{4}$x0.此时快速向左拨动管子,钢珠恰好在管子竖直时从管口飞出,并垂直击中正前方的目标靶靶心.已知目标靶靶心离竖直杆顶的水平距离为L,竖直距离为$\frac{L}{2}$,试分析: P、Q是一列简谐横波中的质点,相距30m,各自的振动图象如图所示.
P、Q是一列简谐横波中的质点,相距30m,各自的振动图象如图所示.