��Ŀ����
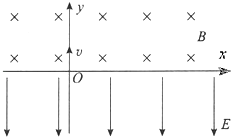
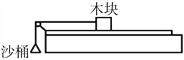
����Ŀ�������δ��ʹ���1m/s���ٶ���ʱ������ת�������ߵĴ��ʹ�������2m����ˮƽ����ļнǾ�Ϊ37������������С���A��B�Ӵ��ʹ����˶���1m/s�ij��ٶ��ش��ʹ��»�������봫�ʹ���Ķ�Ħ����������0.5����gȡ10m/s2�� ![]() =0.6��
=0.6�� ![]() =0.8������˵����ȷ������ ��
=0.8������˵����ȷ������ ��
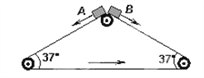
A. ���A�ȵ��ﴫ�ʹ���
B. ���A��B�ļ��ٶ�֮��Ϊ![]() ��1
��1
C. ���A��B���ﴫ�ʹ���ʱ�ٶȴ�С���
D. ���A��B�ڴ��ʹ��ϵĻ��۳���֮��Ϊ1��3
���𰸡�CD
��������AB������A������֪��A�����������»��������ڻ���Ħ�������������Ƥ�����¼��٣����ٶ�Ϊ�� ![]() ������B��������֪��B�����Ƥ��Ҳ�����»��ģ�Ħ�������ϣ�����ٶ�Ҳ����Ϊ��
������B��������֪��B�����Ƥ��Ҳ�����»��ģ�Ħ�������ϣ�����ٶ�Ҳ����Ϊ�� ![]() ���ɼ���������ļ��ٶ���ͬ������λ��һ�������˶�ѧ��ʽ
���ɼ���������ļ��ٶ���ͬ������λ��һ�������˶�ѧ��ʽ![]() ֪��AB�����廬����ʱʱ����ͬ����AB����
֪��AB�����廬����ʱʱ����ͬ����AB����
C����![]() ��֪����˵��ٶ���ͬ��C��ȷ��
��֪����˵��ٶ���ͬ��C��ȷ��
D�����۳��������λ�ƾ����������Ϸ���![]() ������ü��ٶ�Ϊ
������ü��ٶ�Ϊ![]() ������
������![]() �������ʱ��Ϊt=1s��A�����봫�ʹ��˶�������ͬ��
�������ʱ��Ϊt=1s��A�����봫�ʹ��˶�������ͬ�� ![]() ��B����Ļ���Ϊ��
��B����Ļ���Ϊ�� ![]() �������A��B�ڴ��ʹ��ϵĻ��۳���֮��Ϊ1:3����D��ȷ��
�������A��B�ڴ��ʹ��ϵĻ��۳���֮��Ϊ1:3����D��ȷ��
��ѡCD��

��ϰ��ϵ�д�
�����Ŀ