题目内容
 如图所示,两平行金属板水平放置,板间存在竖直向下的勻强电场.一带电粒子以初速度V0沿上板边缘垂直于电场线射入匀强电场,它刚好贴着下板边缘飞出.已知匀强电场两极板长L,间距为d,(粒子的重力忽略不计)求:
如图所示,两平行金属板水平放置,板间存在竖直向下的勻强电场.一带电粒子以初速度V0沿上板边缘垂直于电场线射入匀强电场,它刚好贴着下板边缘飞出.已知匀强电场两极板长L,间距为d,(粒子的重力忽略不计)求:(1)如果带电粒子的初速度变为2V0,则离开电场时,沿场强方向的侧向位移y为多少?
(2)如果带电粒子的初速度变为2V0,粒子离开电场后继续运动,当它的竖直位移仍为d时,它的水平位移x为多少?
(3)如果带电粒子的初速度变为2V0,粒子离开电场时动能与带电粒子以初速度V0射入匀强电场后离开电场时动能之比?
分析:(1)带电粒子垂直于电场线射入匀强电场,只受电场力作用,做类平抛运动.根据运动学公式分别列出水平位移和竖直位移表达式,运用比例法,求出初速度变为2V0,粒子离开电场时,沿场强方向的侧向位移y.
(2)粒子离开电场后速度反向延长线交上板的中点,根据三角知识求出速度偏向角与位移、板长的关系,再求出水平位移x.
(3)根据动能定理分别两种情况下粒子离开电场时的动能,再结合初动能与板间电压的关系,求解粒子离开电场时动能之比.
(2)粒子离开电场后速度反向延长线交上板的中点,根据三角知识求出速度偏向角与位移、板长的关系,再求出水平位移x.
(3)根据动能定理分别两种情况下粒子离开电场时的动能,再结合初动能与板间电压的关系,求解粒子离开电场时动能之比.
解答: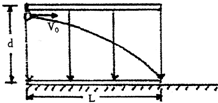 解:
解:
(1)带电粒子的初速度为v0时,
水平方向:L=v0t1
竖直方向:d=
a
联立得到,d=
a(
)2
带电粒子的初速度变为2V0时,
水平方向:L=2v0t2
竖直方向:y=
a
联立得到,y=
a(
)2=
d
(2)带电粒子的初速度变为2v0,粒子离开电场时速度的偏向角为φ.根据推论可知,粒子离开电场时速度的反向延长线交于上板的中点.则根据几何知识有
tanφ=
=
,又tanφ=
解得 LAB=2L
所以x=0.5L+LAB=2.5L
(3)根据动能定理得,
由第(1)问d=
a(
)2,a=
得
联立解得:
=
答:
(1)带电粒子的初速度变为2V0,离开电场时,沿场强方向的侧向位移y为
d.
(2)带电粒子的初速度变为2V0,粒子离开电场后继续运动,当它的竖直位移仍为d时,它的水平位移x为2.5L.
(3)如果带电粒子的初速度变为2V0,粒子离开电场时动能与带电粒子以初速度V0射入匀强电场后离开电场时动能之比
=
.
 解:
解:(1)带电粒子的初速度为v0时,
水平方向:L=v0t1
竖直方向:d=
| 1 |
| 2 |
| t | 2 1 |
联立得到,d=
| 1 |
| 2 |
| L |
| v0 |
带电粒子的初速度变为2V0时,
水平方向:L=2v0t2
竖直方向:y=
| 1 |
| 2 |
| t | 2 2 |
联立得到,y=
| 1 |
| 2 |
| L |
| 2v0 |
| 1 |
| 4 |
(2)带电粒子的初速度变为2v0,粒子离开电场时速度的偏向角为φ.根据推论可知,粒子离开电场时速度的反向延长线交于上板的中点.则根据几何知识有
tanφ=
| ||
|
| d |
| 2L |
| d |
| LAB |
解得 LAB=2L
所以x=0.5L+LAB=2.5L
(3)根据动能定理得,
|
由第(1)问d=
| 1 |
| 2 |
| L |
| v0 |
| qu |
| md |
|
联立解得:
| Ek2 |
| Ek1 |
| d2+4L2 |
| 4d2+L2 |
答:
(1)带电粒子的初速度变为2V0,离开电场时,沿场强方向的侧向位移y为
| 1 |
| 4 |
(2)带电粒子的初速度变为2V0,粒子离开电场后继续运动,当它的竖直位移仍为d时,它的水平位移x为2.5L.
(3)如果带电粒子的初速度变为2V0,粒子离开电场时动能与带电粒子以初速度V0射入匀强电场后离开电场时动能之比
| Ek2 |
| Ek1 |
| d2+4L2 |
| 4d2+L2 |
点评:本题是类平抛运动问题,应用了力学中牛顿第二定律、运动学公式、动能定理等多个规律.对于第(2)问也可以根据三角形相似法求出水平位移.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
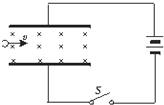 如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )
如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )| A、把两板间距离减小一半,同时把粒子速率增加一倍 | B、把两板的距离增大一倍,同时把板间的磁感应强度增大一倍 | C、把开关S断开,两板的距离增大一倍,同时把板间的磁感应强度减为一半 | D、把开关S断开,两板的距离减小一半,同时把粒子速率减小一半 |
 如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )
如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )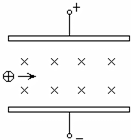 如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( )
如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( ) 如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( )
如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( ) 如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=
如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=