题目内容
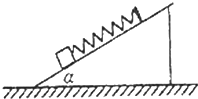 质量为m的小物块,用轻弹簧固定在光滑的斜面体上,斜面的倾角为α,如图所示.使小物块和斜面体一起由静止开始向右做加速运动,加速度从零逐渐缓慢增大,已知轻弹簧的劲度系数为k,重力加速度用g表示.求:
质量为m的小物块,用轻弹簧固定在光滑的斜面体上,斜面的倾角为α,如图所示.使小物块和斜面体一起由静止开始向右做加速运动,加速度从零逐渐缓慢增大,已知轻弹簧的劲度系数为k,重力加速度用g表示.求:
(1)加速度为零时,弹簧的伸长量?
(2)小物块对斜面体的压力为零时,斜面体向右的加速度?
解:(1)开始时,小物块的加速度为零时,有:
mgsinα=kx
解得此时弹簧的伸长量x=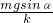
(2)当小物块对斜面压力为零时,对物块受力分析可知其合力为mgcotα
由牛顿第二定律:mgcotα=ma
解得 a=g-cotα
由于物块和斜面体是一个整体,且相对静止,故斜面体的加速度也为mgcotα
答:
(1)加速度为零时,弹簧的伸长量: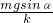
(2)小物块对斜面体的压力为零时,斜面体向右的加速度g-cotα
分析:(1)由加速度为零,可知,重力的分力与弹力相等,故可以求得伸长量
(2)物体对斜面体压力为零时,其合力为mgcotα,由此可以求得物体的加速度,也等于斜面体的加速度.
点评:本题难点在第二问,我们要对物块受力分析,通过求得物块的加速度,来找斜面体的加速度,这种情况只适用于两者相对静止.其余不适用.
mgsinα=kx
解得此时弹簧的伸长量x=
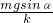
(2)当小物块对斜面压力为零时,对物块受力分析可知其合力为mgcotα
由牛顿第二定律:mgcotα=ma
解得 a=g-cotα
由于物块和斜面体是一个整体,且相对静止,故斜面体的加速度也为mgcotα
答:
(1)加速度为零时,弹簧的伸长量:
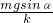
(2)小物块对斜面体的压力为零时,斜面体向右的加速度g-cotα
分析:(1)由加速度为零,可知,重力的分力与弹力相等,故可以求得伸长量
(2)物体对斜面体压力为零时,其合力为mgcotα,由此可以求得物体的加速度,也等于斜面体的加速度.
点评:本题难点在第二问,我们要对物块受力分析,通过求得物块的加速度,来找斜面体的加速度,这种情况只适用于两者相对静止.其余不适用.

练习册系列答案
相关题目
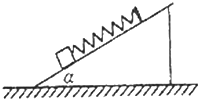 质量为m的小物块,用轻弹簧固定在光滑的斜面体上,斜面的倾角为α,如图所示.使小物块和斜面体一起由静止开始向右做加速运动,加速度从零逐渐缓慢增大,已知轻弹簧的劲度系数为k,重力加速度用g表示.求:
质量为m的小物块,用轻弹簧固定在光滑的斜面体上,斜面的倾角为α,如图所示.使小物块和斜面体一起由静止开始向右做加速运动,加速度从零逐渐缓慢增大,已知轻弹簧的劲度系数为k,重力加速度用g表示.求: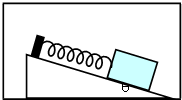 质量为m的小物块,用轻弹簧固定在斜面体上,斜面的倾角为θ,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.
质量为m的小物块,用轻弹簧固定在斜面体上,斜面的倾角为θ,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.
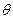 ,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.
,轻弹簧的劲度系数为k,如图所示.整个装置放在电梯内.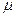 ,弹簧的伸长量也为2 x,求此时电梯上升加速度的最大值.(设最大静摩擦力与滑动摩擦力大小相等)
,弹簧的伸长量也为2 x,求此时电梯上升加速度的最大值.(设最大静摩擦力与滑动摩擦力大小相等)