Question

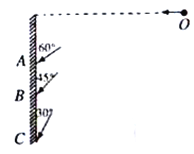
【题目】某马戏团演员做滑杆表演时，所用竖直滑杆的上端通过拉力传感器固定在支架上，下端悬空，滑杆的质量为20 kg。从演员在滑杆上端做完动作时开始计时，演员先在杆上静止了0.5 s，然后沿杆下滑，3.5 s末刚好滑到杆底端，速度恰好为零，整个过程演员的 图象和传感器显示的拉力随时间的变化情况分别如图甲、乙所示，取重力加速度g=10m／s2，则下列说法正确的是

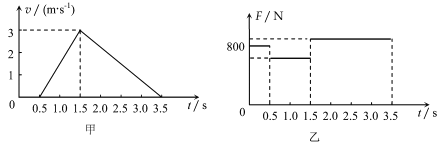
A. 演员在1.0 s时的加速度大小为2m／s2 B. 滑杆的长度为5.25 m

C. 传感器显示的最小拉力为420 N D. 3.5 s内演员损失的机械能为2700 J

Answer 1

【答案】D

【解析】

根据图象可明确演员的运动情况，明确加速度的方向，再根据v-t图象与时间轴的面积可表示位移；根据牛顿第二定律可确定杆受到的拉力．3.5 s内演员速度不变，减小的重力势能等于损失的机械能。

A. 由v-t图像可知，演员在1.0 s时的加速度大小a= m／s2=3m／s2，故A错误；

B.vt图象的面积表示位移，则可知，总长度x= ×3×3=4.5m，故B错误；

C. 两图结合可知，静止时，传感器示数为800N，除去杆的重力200N，演员的重力就是600N，在演员加速下滑阶段，处于失重状态，杆受到的拉力最小，由牛顿第二定律得：mgF1=ma，

解得：F1=420N，加上杆的重力200N，可知杆受的拉力为620N，故C错误；

D. 3.5 s内演员速度不变，减小的重力势能等于损失的机械能为△E=mgh=600×4.5J=2700J，故D正确。

故选：D.