题目内容
如图甲所示，在真空中足够大的绝缘水平地面上，一个质量为m=0.2kg，带电量为q=+2.0×10-6C的小物块处于静止状态，小物块与地面间的动摩擦因数μ=0.1．从t=0时刻开始，空间加上一个如图乙所示的场强大小和方向呈周期性变化的电场，以下说法正确的是．（取水平向右为正方向，g取10m/s2．）（ ）
分析：小物块在水平地面上受电场力和摩擦力，根据物体的受力判断物体的运动，根据运动学公式求出物体的速度和位移．
解答：解：0～2s内，电场力F=qE=2.0×10-6×3×105=0.6N＞μmg，物块做匀加速直线运动，加速度a=
=
m/s2=2m/s2，2s末的速度为v=at=4m/s．2～4内电场力反向，加速度a′=
=
m/s2=2m/s2，做匀减速直线运动，4s末速度为零，然后又重复以前的运动．15s末的速度与3s末的速度相等，大小v′=4-2m/s=2m/s，方向向右．
在0～2s内的位移x=
at2=
×2×4m=4m，所以14s内的位移为4×7m=28m，最后1s内的位移x′=vt′-
at′2=4-1m=3m，所以15秒内小物块的位移大小31m．故A、D正确，B、C错误．
故选AD．
| F-f |
| m |
| 0.6-0.2 |
| 0.2 |
| F′+f |
| m |
| 0.2+0.2 |
| 0.2 |
在0～2s内的位移x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选AD．
点评：解决本题的关键能够正确地进行受力分析，通过物体的受力，判断物体的运动，结合牛顿第二定律和运动学公式进行求解．
练习册系列答案
相关题目
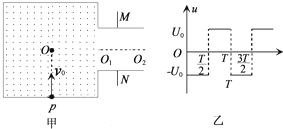如图甲所示，在真空中，有一边长为a的正方形区域内存在匀强磁场，磁场方向垂直纸面向外．在磁场右侧有一对平行金属板M和N，两板间距及板长均为b，板间的中心线O1O2与正方形的中心O在同一直线上．有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场，从正方形右侧O1点水平飞出磁场时，立即给M、N两板加上如图乙所示的交变电压，最后粒子刚好以平行于M板的速度从M板的边缘飞出．（不计粒子所受到的重力、两板正对面之间为匀强电场，边缘电场不计） 
时，该粒子从MN板右侧沿板的中心线，仍以速度v0射入M、N之间，求粒子从磁场中射出的点到a点的距离。
时刻，该粒子从M、N板右侧沿板的中心线仍以速率v0向左射入M、N之间，求粒子从磁场中射出的点到a点的距离。
