题目内容
如图甲所示，在真空中，半径为R的圆形区域内存在匀强磁场，磁场方向垂直纸面向外。在磁场右侧有一对平行金属板M和N，两板间距离为R，板长为2R，板的中心线O1O2与磁场的圆心O在同一直线上。有一电荷量为q、质量为m的带正电的粒子，以速度v0从圆周上的a点沿垂直于半径OO1并指向圆心的方向进入磁场，当从圆周上的O1点飞出磁场时，给M、N板加上如图乙所示电压，最后粒子刚好以平行于N板的速度从N板的边缘飞出(不计粒子重力)。(1)求磁场的磁感应强度B。
(2)求交变电压的周期T和电压U0的值。
(3)若在t=
时，该粒子从MN板右侧沿板的中心线，仍以速度v0射入M、N之间，求粒子从磁场中射出的点到a点的距离。
(1)B= (2)T=
U0=
(n=1,2,…) (3)d=2R
解析：(1) 粒子自a点进入磁场，从O1点水平飞出磁场，运动的轨道半径为R。则
qBv0=
(2)粒子自O1点进入电场，最后恰好从N板的边缘平行极板飞出，设运动时间为t，则2R=v0t
=2n·
t=nT(n=1,2,…)
解得：T=
，U0=
(n=1,2,…)
(3)当t=
时，粒子以速度v0沿O2O1射入电场，则该粒子恰好从M板边缘以平行于极板的速度射入磁场，进入磁场的速度仍为v0，运动的轨道半径为R设进入磁场时的点为b，离开磁场时的点为c，圆心为O3，如图所示，四边形ObO
练习册系列答案
相关题目
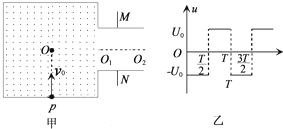如图甲所示，在真空中，有一边长为a的正方形区域内存在匀强磁场，磁场方向垂直纸面向外．在磁场右侧有一对平行金属板M和N，两板间距及板长均为b，板间的中心线O1O2与正方形的中心O在同一直线上．有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场，从正方形右侧O1点水平飞出磁场时，立即给M、N两板加上如图乙所示的交变电压，最后粒子刚好以平行于M板的速度从M板的边缘飞出．（不计粒子所受到的重力、两板正对面之间为匀强电场，边缘电场不计） 
时刻，该粒子从M、N板右侧沿板的中心线仍以速率v0向左射入M、N之间，求粒子从磁场中射出的点到a点的距离。
