题目内容
20. 如图为一回旋加速器的示意图,已知D形盒的半径为R,中心O处放有质量为m、带电量为q的正离子源,若磁感应强度大小为B,求:
如图为一回旋加速器的示意图,已知D形盒的半径为R,中心O处放有质量为m、带电量为q的正离子源,若磁感应强度大小为B,求:(1)加在D形盒间的高频电源的频率$\frac{qB}{2πm}$;
(2)离子加速后的最大能量$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$;
(3)离子在第n次通过窄缝前后的半径之比$\frac{{r}_{n-1}}{{r}_{n}}=\sqrt{\frac{n-1}{n}}$.
分析 (1)根据质子做匀速圆周运动的周期公式,即可求解;
(2)根据运动半径等于R,结合牛顿第二定律与向心力,即可求解;
(3)根据加速后最大动能,结合加速次数,从而可确定加速与回旋时间.
解答 解:(1)质子的回旋周期为:$T=\frac{2πR}{v}=\frac{2πm}{qB}$①
高频电源的频率为:$f=\frac{1}{T}=\frac{qB}{2πm}$②
(2)当回旋半径r=R时,质子的速度最大
$q{v_m}B=m\frac{v_m^2}{R}$
得${v_m}=\frac{qBR}{m}$③
质子加速后的最大动能为:${E_k}=\frac{1}{2}mv_m^2=\frac{{{q^2}{B^2}{R^2}}}{2m}$④
(3)质子在电场中加速的次数为n-1次后,则:Ekn-1=(n-1)•qU ⑤
质子在电场中加速的次数为n次后,则:Ekn=n•qU ⑥
由洛伦兹力提供向心力得:$qvB=\frac{m{v}^{2}}{R}$
得:R=$\frac{mv}{qB}$ ⑦
所以:$\frac{{R}_{n-1}}{{R}_{n}}=\frac{{v}_{n-1}}{n}$=$\sqrt{\frac{{E}_{kn-1}}{{E}_{kn}}}=\sqrt{\frac{(n-1)qU}{nqU}}$=$\sqrt{\frac{n-1}{n}}$
故答案为:(1)$\frac{qB}{2πm}$;(2)$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$;(3)$\frac{{r}_{n-1}}{{r}_{n}}=\sqrt{\frac{n-1}{n}}$
点评 考查粒子做匀速圆周的周期公式与半径公式的应用,掌握牛顿第二定律,注意区别求加速时间与回旋时间的不同.

 口算能手系列答案
口算能手系列答案| A. | 雨滴下落的时间会变长 | B. | 雨滴落地的速度回变大 | ||
| C. | 落地时雨滴重力的功率会变大 | D. | 雨滴落地时的机械能会变大 |
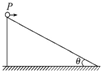 如图所示,斜面倾角为θ,从斜面的P点分别以v0和2v0的速度水平抛出A、B两个小球,不计空气阻力,若两小球均落在斜面上且不发生反弹,则( )
如图所示,斜面倾角为θ,从斜面的P点分别以v0和2v0的速度水平抛出A、B两个小球,不计空气阻力,若两小球均落在斜面上且不发生反弹,则( )| A. | A、B两球飞行时间之比为1:2 | |
| B. | A、B两球的水平位移之比为4:1 | |
| C. | A、B下落的高度之比为1:2 | |
| D. | A、B两球落到斜面上的速度大小之比为1:4 |
| A. | |$\overline{F}$|=$\frac{|\overline{G}|}{2cosθ}$ | B. | |$\overline{F}$|=$\frac{\overline{G}}{2sinθ}$ | C. | $\overline{F}$=$\frac{\overline{G}}{2cos\frac{θ}{2}}$ | D. | |$\overline{F}$|=$\frac{|\overline{G}|}{2cos\frac{θ}{2}}$ |
| A. | 力一定是成对出现的 | |
| B. | 一对作用力与反作用力其中一个力是动力,另一个力一定是阻力 | |
| C. | 一对作用力与反作用力可以同时是阻力 | |
| D. | 弹力是摩擦力产生的必要条件 |
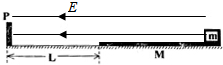 光滑水平面上有一质量为M=2kg的足够长的绝缘木板,木板上最右端有一可视为质点的带正电q=6.0×10-3C质量为m=3kg的物块,物块与木板间的动摩擦因数μ=0.4,且最大静摩擦力等于滑动摩擦力.开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P.现加一水平向左的匀强电场E=1.0×103N/C,若木板与挡板P发生撞击时间极短,并且撞击时无动能损失,物块始终未能与挡板相撞,取g=10m/s2,求:
光滑水平面上有一质量为M=2kg的足够长的绝缘木板,木板上最右端有一可视为质点的带正电q=6.0×10-3C质量为m=3kg的物块,物块与木板间的动摩擦因数μ=0.4,且最大静摩擦力等于滑动摩擦力.开始时物块和木板都静止,距木板左端L=2.4m处有一固定在水平面上的竖直弹性挡板P.现加一水平向左的匀强电场E=1.0×103N/C,若木板与挡板P发生撞击时间极短,并且撞击时无动能损失,物块始终未能与挡板相撞,取g=10m/s2,求: 如图所示,一根橡皮筋上端固定在悬点A,当它自由下垂时,下端恰好能达到O处,今在O处垂直橡皮筋钉一个光滑的小钉子,当橡皮筋的下端挂上一个重物,重物下降10cm后静止于水平地面,小钉子恰好能挡在橡皮筋的右侧,若用水平力F使重物缓慢向右移动,初始时,水平力F1=9N即可使之移动.当橡皮筋与水平面成夹角θ=30°时,使之缓慢移动的水平力变为F2=(9+10$\sqrt{3}$)N.已知水平面上与重物的摩擦因数μ=0.1,且橡皮筋在此过程中严格遵守胡克定律,g=10m/s2,设滑动摩擦力与最大静摩擦力相等,求重物的质量m和橡皮筋的劲度系数k.
如图所示,一根橡皮筋上端固定在悬点A,当它自由下垂时,下端恰好能达到O处,今在O处垂直橡皮筋钉一个光滑的小钉子,当橡皮筋的下端挂上一个重物,重物下降10cm后静止于水平地面,小钉子恰好能挡在橡皮筋的右侧,若用水平力F使重物缓慢向右移动,初始时,水平力F1=9N即可使之移动.当橡皮筋与水平面成夹角θ=30°时,使之缓慢移动的水平力变为F2=(9+10$\sqrt{3}$)N.已知水平面上与重物的摩擦因数μ=0.1,且橡皮筋在此过程中严格遵守胡克定律,g=10m/s2,设滑动摩擦力与最大静摩擦力相等,求重物的质量m和橡皮筋的劲度系数k.