题目内容
11.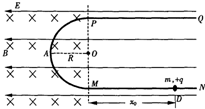 如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感强度大小为B.一绝缘弯杆由两段直杆和一段半径为R的半圆环组成,固定在纸面所在的竖直平面内.PQ、MN水平且足够长,半圆环PAM在磁场边界左侧,P、M点在磁场边界线上,NMAP段是光滑的,现有一质量为m 、带电+q的小环套在MN杆上,它所受电场力为重力的$\frac{3}{4}$倍.现在M右侧D点由静止释放小环,小环刚好能到达P点.
如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感强度大小为B.一绝缘弯杆由两段直杆和一段半径为R的半圆环组成,固定在纸面所在的竖直平面内.PQ、MN水平且足够长,半圆环PAM在磁场边界左侧,P、M点在磁场边界线上,NMAP段是光滑的,现有一质量为m 、带电+q的小环套在MN杆上,它所受电场力为重力的$\frac{3}{4}$倍.现在M右侧D点由静止释放小环,小环刚好能到达P点. (1)求DM间距离x0 ;
(2)求上述过程中小环第一次通过与O等高的A点时弯杆对小环作用力的大小;
(3)若小环与PQ间动摩擦因数为m (设最大静摩擦力与滑动摩擦力大小相等),现将小环移至M 点右侧4R处由静止开始释放,求小环在整个运动过程中克服摩擦力所做的功.
分析 (1)对D到P为研究过程,运用动能定理求出DM间的距离.
(2)对D到A为研究过程,运用动能定理求出A点的速度,根据牛顿第二定律,沿半径方向上合力提供向心力,求出弯杆对小环作用力的大小.
(3)需讨论摩擦力的大小与电场力的大小关系,若摩擦力大于电场力,则运动到P点右侧停止;若摩擦力小于电场力,则环最终在DP间往复运动.根据动能定理求出摩擦力做的功.
解答 解:(1)小环刚好到达P点时速度:vP =0,
由动能定理得:qEx0-2mgR=0 ①
由题意可知:qE=$\frac{3}{4}$mg ②
由①②解得:x0=$\frac{8R}{3}$;
(2)设小环在A点时的速度为vA ,由动能定理得:
qE(x0+R)-mgR=$\frac{1}{2}$mv${\;}_{A}^{2}$-0 ③
解得:vA=$\frac{\sqrt{14Rg}}{2}$ ④
设小环在A点时所受弯杆的作用力大小为N ,
由牛顿第二定律得:N-qvAB-qE=m$\frac{{{v}_{A}}^{2}}{R}$ ⑤
由②、④、⑤得N=$\frac{17mg}{4}+\frac{qB\sqrt{14Rg}}{2}$;
(3)若f=μmg ≥qE ,即:μ≥$\frac{3}{4}$,
小环第一次到达P点右侧sl 距离处静止,
由动能定理得:qE(4R-s1)-2mgR-fs1=0 ⑥
滑动摩擦力:f=μmg ⑦
由⑥、⑦得s1=$\frac{4R}{4μ+3}$ ⑧
克服摩擦力所做的功W=fs1=$\frac{4μmgR}{4μ+3}$ ⑨
若f=mg <qE ,即μ<$\frac{3}{4}$,环经过来回往复运动一段时间之后,最后只能在光滑的PD之间往复运动,设克服摩擦力功为W,则:
qE(4R)-2mgR-W=0 ⑩
解得:W=mgR;
答:(1)DM间距离x0 为$\frac{8R}{3}$;
(2)上述过程中小环第一次通过与O等高的A点时弯杆对小环作用力的大小为$\frac{17mg}{4}+\frac{qB\sqrt{14Rg}}{2}$;
(3)小环在整个运动过程中克服摩擦力所做的功为$\frac{4μmgR}{4μ+3}$或mgR.
点评 本题是一道力学综合题,分析清楚物体运动过程是正确解题的关键,运用动能定理解题需合适地选取研究的过程,根据动能定理列出表达式求解.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 如图所示,在匀强电场中,过O点作线段OA=OB=OC=OD=10cm.已知O、A、B、C、D各点的电势分别为0、7V、8V、7V、5V,则匀强电场的场强大小和方向最接近于( )
如图所示,在匀强电场中,过O点作线段OA=OB=OC=OD=10cm.已知O、A、B、C、D各点的电势分别为0、7V、8V、7V、5V,则匀强电场的场强大小和方向最接近于( )| A. | 70V/m,沿OA方向 | B. | 70V/m,沿OC方向 | C. | 80V/m,沿OB方向 | D. | 80V/m,沿BO方向 |
| A. | 使一定质量的理想气体(不计分子势能的气体)等压压缩,其内能一定减小 | |
| B. | 布朗运动是悬浮在液体中的固体分子的运动 | |
| C. | 热量有可能自发地从低温物体传到高温物体 | |
| D. | 破镜难圆是因为分于间有斥力 |
| A. | 飞行方向相同,但加油机的速度大 | B. | 飞行方向相同,但加油机的速度小 | ||
| C. | 飞行方向相同,并且速度大小相等 | D. | 飞行方向相反,并且速度大小相等 |
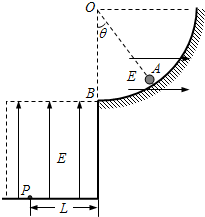 如图,绝缘的光滑圆弧曲面固定在竖直平面内,B为曲面最低点.曲面上的A点与曲面圆心O的连线与竖直方向成夹角θ=37°.曲面所在区域和B点左下方的区域内都存在电场强度大小都为E的匀强电场,方向分别是水平向右和竖直向上.开始时有一质量为m的带电小球处于A点恰好保持静止.此后将曲面内的电场撤去,小球沿曲面下滑至B点时以大小为v0的速度水平抛出,最后落在电场内地面的P点,P点与B点间的水平距离为L. 已知tan37°=0.75,重力加速度为g,求:
如图,绝缘的光滑圆弧曲面固定在竖直平面内,B为曲面最低点.曲面上的A点与曲面圆心O的连线与竖直方向成夹角θ=37°.曲面所在区域和B点左下方的区域内都存在电场强度大小都为E的匀强电场,方向分别是水平向右和竖直向上.开始时有一质量为m的带电小球处于A点恰好保持静止.此后将曲面内的电场撤去,小球沿曲面下滑至B点时以大小为v0的速度水平抛出,最后落在电场内地面的P点,P点与B点间的水平距离为L. 已知tan37°=0.75,重力加速度为g,求: 如图所示,半径为0.4m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的最低点A.一质量为0.1kg的物体,以初速度v0=7.0m/s在水平面上向左运动,物体与地面的动摩擦因数为0.3,运动4.0m后,冲上竖直半圆环,最后物体落在C点,求:
如图所示,半径为0.4m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的最低点A.一质量为0.1kg的物体,以初速度v0=7.0m/s在水平面上向左运动,物体与地面的动摩擦因数为0.3,运动4.0m后,冲上竖直半圆环,最后物体落在C点,求: 设处于如图所示坐标原点处的振源振动方程为y=4sinπt cm,如果从振源起振开始计时,测得t=5s时刻,位于坐标X=10m的X轴上的质点P开始起振.根据这些条件几个同学通过分析计算作出以下判断:
设处于如图所示坐标原点处的振源振动方程为y=4sinπt cm,如果从振源起振开始计时,测得t=5s时刻,位于坐标X=10m的X轴上的质点P开始起振.根据这些条件几个同学通过分析计算作出以下判断: 如图,在磁感应强度为B、方向垂直纸面向里的匀强磁场中,金属杆MN在平行金属导轨上以速度v向右匀速滑动,MN中产生的感应电动势为El;若磁感应强度增为2B,其他条件不变,MN中产生的感应电动势变为E2.则通过电阻R的电流方向是c→a,E1与E2之比=1:2..
如图,在磁感应强度为B、方向垂直纸面向里的匀强磁场中,金属杆MN在平行金属导轨上以速度v向右匀速滑动,MN中产生的感应电动势为El;若磁感应强度增为2B,其他条件不变,MN中产生的感应电动势变为E2.则通过电阻R的电流方向是c→a,E1与E2之比=1:2..