题目内容
6. 设处于如图所示坐标原点处的振源振动方程为y=4sinπt cm,如果从振源起振开始计时,测得t=5s时刻,位于坐标X=10m的X轴上的质点P开始起振.根据这些条件几个同学通过分析计算作出以下判断:
设处于如图所示坐标原点处的振源振动方程为y=4sinπt cm,如果从振源起振开始计时,测得t=5s时刻,位于坐标X=10m的X轴上的质点P开始起振.根据这些条件几个同学通过分析计算作出以下判断:①这一列波的波长为2m
②t=5s时刻平衡位置位于坐标原点处的质点正通过平衡位置沿y轴负方向运动.
③t=5s时刻平衡位置位于坐标X=6.5m处的质点关于平衡位置的位移是沿y轴负方向,速度也是沿为y轴负方向.
④从波源起振到t=5s这一段时间内平衡位置位于坐标X=7m处的质点通过的路程是12cm
以上正确的结果是( )
| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
分析 根据振动方程通式与题中的振动方程对应起来可求出周期,由v=$\frac{X}{t}$求出波速,根据“上下坡”法判断波的传播方向
解答 解:①由振动方程可知,ω=π,则周期:$T=\frac{2π}{ω}=\frac{2π}{π}=2$s,波速v=$\frac{X}{t}=\frac{10}{5}=2$m/s,该波的波长:λ=vT=2×2=4m.故①错误;
②由波源的振动方程可知,波源起振的方向向上,t=5s=$2\frac{1}{2}$T,此时平衡位置位于坐标原点处的质点正通过平衡位置沿y轴负方向运动.故②正确;
③该波传播到坐标X=6.5m处的时间:$t′=\frac{x}{v}=\frac{6.5}{2}=3.25$s
到t=5s时刻,质点振动的时间:△t=5-3.25=1.75s=$\frac{7}{8}$T$>\frac{3}{4}$T,此时质点正从负向的最大位移处向平衡位置处运动,速度的方向为正方向.故③错误;
④该波传播到坐标X=7m处的时间:$t″=\frac{x′}{v}=\frac{7}{2}=3.5$s;到t=5s时刻,质点振动的时间:△t′=5-3.5=1.5s=$\frac{3}{4}T$;由于质点在一个周期内的路程是4A,所以这一段时间内平衡位置位于坐标X=7m处的质点通过的路程是S=3A=3×4=12cm.故④正确.
故选:D
点评 本题考查波的传播及波长、波速及频率的关系,要注意学会根据传播距离及传播时间求解波速.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
19.如图所示为电场中的一条电场线,A、B为其上的两点,以下说法正确的是( )
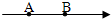
| A. | EA与EB一定不等,ϕA与ϕB一定不等 | B. | EA与EB可能相等,ϕA一定高于ϕB | ||
| C. | EA与EB一定不等,ϕA与ϕB可能相等 | D. | EA与EB可能相等,ϕA与ϕB可能相等 |
1. 如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则( )
如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则( )
 如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则( )
如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则( )| A. | 小球A与B之间库仑力的大小为2$\frac{{k{q^2}}}{d^2}$ | |
| B. | 当$\frac{q}{d}$=$\sqrt{\frac{mgsinθ}{k}}$时,细线上的拉力为0 | |
| C. | 当$\frac{q}{d}$=$\sqrt{\frac{mgtanθ}{k}}$时,细线上的拉力为0 | |
| D. | 当$\frac{q}{d}$=$\sqrt{\frac{mg}{ktanθ}}$时,斜面对小球A的支持力为0 |
18.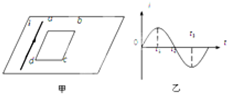 如甲图所示,光滑的水平桌面上固定着一根绝缘的长直导线,可以自由移动的矩形导线框abcd靠近长直导线静放在桌面上.当长直导线中的电流按乙图所示的规律变化时(甲图中电流所示的方向为正方向),下述正确的是( )
如甲图所示,光滑的水平桌面上固定着一根绝缘的长直导线,可以自由移动的矩形导线框abcd靠近长直导线静放在桌面上.当长直导线中的电流按乙图所示的规律变化时(甲图中电流所示的方向为正方向),下述正确的是( )
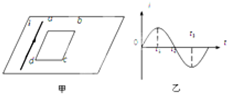 如甲图所示,光滑的水平桌面上固定着一根绝缘的长直导线,可以自由移动的矩形导线框abcd靠近长直导线静放在桌面上.当长直导线中的电流按乙图所示的规律变化时(甲图中电流所示的方向为正方向),下述正确的是( )
如甲图所示,光滑的水平桌面上固定着一根绝缘的长直导线,可以自由移动的矩形导线框abcd靠近长直导线静放在桌面上.当长直导线中的电流按乙图所示的规律变化时(甲图中电流所示的方向为正方向),下述正确的是( )| A. | 0~t1时间内,线框内电流方向为adcba,线框向右减速运动 | |
| B. | t1时刻,线框内没有电流,线框静止 | |
| C. | t1~t2时间内,线框内电流的方向为abcda,线框向左运动 | |
| D. | 在t2时刻,线框内有电流 |
15. 两块水平放置的金属板和两个可变电阻及电源连成如图所示的电路,闭合开关之后,有一个质量为M的带电油滴悬浮在两板之间不动.要使油滴上升,可采用的办法是( )
两块水平放置的金属板和两个可变电阻及电源连成如图所示的电路,闭合开关之后,有一个质量为M的带电油滴悬浮在两板之间不动.要使油滴上升,可采用的办法是( )
 两块水平放置的金属板和两个可变电阻及电源连成如图所示的电路,闭合开关之后,有一个质量为M的带电油滴悬浮在两板之间不动.要使油滴上升,可采用的办法是( )
两块水平放置的金属板和两个可变电阻及电源连成如图所示的电路,闭合开关之后,有一个质量为M的带电油滴悬浮在两板之间不动.要使油滴上升,可采用的办法是( )| A. | 减小R1 | B. | 增大R1 | C. | 增大R2 | D. | 减小R2 |
 如图所示是一种悬球式加速度仪.它可以用来测定沿水平轨道做匀加速直线运动的列车的加速度.m是一个金属球,它系在细金属丝的下端,金属丝的上端悬挂在O点,AB是一根长为l的电阻丝,其阻值为R.金属丝与电阻丝接触良好,摩擦不计.电阻丝的中点C焊接一根导线.从O点也引出一根导线,两线之间接入一个电压表V (金属丝和导线电阻不计).图中虚线OC与AB相垂直,且OC=h,电阻丝AB接在电压恒为U的直流稳压电源上.整个装置固定在列车中使AB沿着车前进的方向.列车静止时金属丝呈竖直状态.当列车加速或减速前进时,金属线将偏离竖直方向θ,从电压表的读数变化可以测出加速度的大小.
如图所示是一种悬球式加速度仪.它可以用来测定沿水平轨道做匀加速直线运动的列车的加速度.m是一个金属球,它系在细金属丝的下端,金属丝的上端悬挂在O点,AB是一根长为l的电阻丝,其阻值为R.金属丝与电阻丝接触良好,摩擦不计.电阻丝的中点C焊接一根导线.从O点也引出一根导线,两线之间接入一个电压表V (金属丝和导线电阻不计).图中虚线OC与AB相垂直,且OC=h,电阻丝AB接在电压恒为U的直流稳压电源上.整个装置固定在列车中使AB沿着车前进的方向.列车静止时金属丝呈竖直状态.当列车加速或减速前进时,金属线将偏离竖直方向θ,从电压表的读数变化可以测出加速度的大小.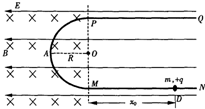 如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感强度大小为B.一绝缘弯杆由两段直杆和一段半径为R的半圆环组成,固定在纸面所在的竖直平面内.PQ、MN水平且足够长,半圆环PAM在磁场边界左侧,P、M点在磁场边界线上,NMAP段是光滑的,现有一质量为m 、带电+q的小环套在MN杆上,它所受电场力为重力的$\frac{3}{4}$倍.现在M右侧D点由静止释放小环,小环刚好能到达P点.
如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感强度大小为B.一绝缘弯杆由两段直杆和一段半径为R的半圆环组成,固定在纸面所在的竖直平面内.PQ、MN水平且足够长,半圆环PAM在磁场边界左侧,P、M点在磁场边界线上,NMAP段是光滑的,现有一质量为m 、带电+q的小环套在MN杆上,它所受电场力为重力的$\frac{3}{4}$倍.现在M右侧D点由静止释放小环,小环刚好能到达P点. 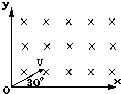 如图所示,在第一象限内有垂直纸面向里的匀强磁场,一对正负电子分别以相同速率沿与X轴成30°角的方向从原点射入磁场,则正、负电子在磁场中运动半径之比为1:1,运动的时间之比为2:1.
如图所示,在第一象限内有垂直纸面向里的匀强磁场,一对正负电子分别以相同速率沿与X轴成30°角的方向从原点射入磁场,则正、负电子在磁场中运动半径之比为1:1,运动的时间之比为2:1.