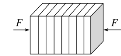
题目内容
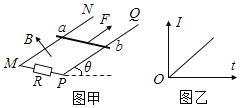
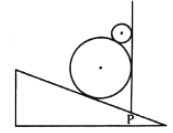
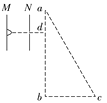
【题目】如图所示,M、N为两平行金属板,其间电压为U。质量为m、电荷量为+q的粒子,从M板由静止开始经电场加速后,从N板上的小孔射出,并沿与ab垂直的方向由d点进入△abc区域,不计粒子重力,已知bc=l,∠c=60°,∠b=90°,ad=![]() l。
l。
(1)求粒子从N板射出时的速度v0;
(2)若△abc区域内存在垂直纸面向外的匀强磁场,要使粒子不从ac边界射出,则磁感应强度最小为多大?
(3)若△abc区域内存在平行纸面且垂直bc方向向下的匀强电场,要使粒子不从ac边界射出,电场强度最小为多大?
【答案】(1) ![]() ; (2)
; (2) ![]() ; (3)
; (3) ![]() ;
;
【解析】试题分析:粒子在加速电场中加速时只有电场力做功,根据动能定理求得粒子射出N时的速度大小;粒子在磁场作用下做匀速圆周运动,作出粒子不从ac边射出时粒子圆周运动的临界轨迹,根据几何关系求得圆周运动的最大半径,再根据洛伦兹力提供圆周运动向心力求得磁感应强度多大;粒子进入电场做类平抛运动,根据要求粒子不从ac边界射出,则粒子到达ac边界时,粒子速度方向与ac边界平行,根据类平抛运动求解即可。
(1)带电粒子在MN间加速,由动能定理可得:![]()
可得粒子从N射出时的速度:![]()
(2)带电粒子在磁场中做匀速圆周运动,磁感应强度越大,粒子做圆周运动的半径越小,当磁感应强度最小时,恰不从ac边界射出粒子到达ac边界时,速度方向沿ac方向,此时粒子不从ac边界射出做圆周运动的最大半径为rm
据洛伦兹力提供圆周运动向心力有:![]()
由几何关系可得,粒子圆周运动的最大半径:![]()
代入解得![]()
即粒子不从ac边界射出时满足![]()
(3)带电粒子在电场中做类平抛运动,电场强度最小为E0时,粒子运动到ac界面的速度方向沿ac方向,设ab和bc方向的位移大小分别为y和x,到达界面时沿ab方向分速度大小为vy,则x=v0t ![]()
又有:vy=v0tan60°
根据几何关系:![]()
解得:![]()
粒子到达ac边界时的速度大小为v则:![]()
根据动能定理有:![]()
解得:![]()

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
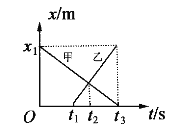
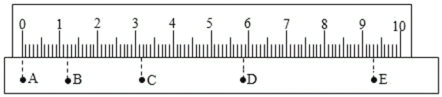
课堂练加测系列答案【题目】如图所示是某同学用打点计时器得到的表示小车运动过程的一条清晰纸带,纸带上两相邻计数点间还有四个点没有画出来,其中x1=7.05cm,x2=7.68cm,x3=8.33cm,x4=8.95cm,x5=9.61cm,x6=10.27cm。

(1)在“练习使用打点计时器”的实验中,下列操作正确的是____________
A.打点前小车应靠近打点计时器,要先接通电源,待计时器开始打点再释放小车
B.要舍去纸带上密集点,然后选取计数点
C.打点频率为50Hz,每四个点取一个计数点,则计数点之间的时间间隔为0.01s
D.实验中应使小车速度尽量小些
(2)推测纸带的运动是做_____运动(选填“加速”、“减速”或者“匀速”)。
(3)下表列出了打点计时器打下B、D、F时小车的瞬时速度,请在表中填入打点计时器打下C、E两点时小车的瞬时速度(保留三位有效数字)。
位置 | B | C | D | E | F |
速度(m·s-1) | 0.737 | ___ | 0.864 | ____ | 0.994 |
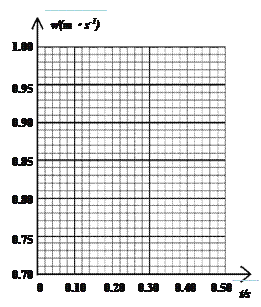
(4)以A点为计时起点,在坐标图中画出小车的速度—时间关系图线_____。
(5)根据你画出的小车的速度—时间的关系图线计算出的小车的加速度a=_________m/s2。(保留两位有效数字)