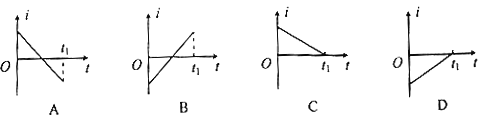题目内容
【题目】电视机的显像管中电子束的偏转是应用磁偏转技术实现的。如左图所示为显像管的原理示意图。显像管中有一个电子枪，工作时阴极发射的电子（速度很小，可视为零）经过加速电场加速后，穿过以O点为圆心、半径为r的圆形磁场区域（磁场方向垂直于纸面），撞击到荧光屏上使荧光屏发光。
已知电子质量为m，电荷量为e，加速电场的电压为U，在没有磁场时电子束通过O点打在荧光屏正中央的M点，OM间距离为S。电子所受的重力、电子间的相互作用力均可忽略不计，也不考虑磁场变化所激发的电场对电子束的作用。由于电子经过加速电场后速度很大，同一电子在穿过磁场的过程中可认为磁场不变。
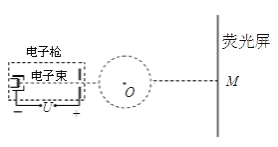
(1)求电子束经偏转磁场后打到荧光屏上时的速率；
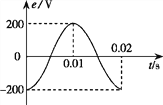
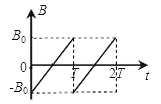
(2)若磁感应强度B随时间变化关系如下图所示，其中
，求电子束打在荧光屏上发光所形成的“亮线”长度。
(3)若其它条件不变，只撤去磁场，利用电场使电子束发生偏转。把正弦交变电压加在一对水平放置的矩形平行板电极上，板间区域有边界理想的匀强电场。电场中心仍位于O点，电场方向垂直于OM。为了使电子束打在荧光屏上发光所形成的“亮线”长度与（2）中相同，问：极板间正弦交变电压的最大值Um、极板长度L、极板间距离d之间需要满足什么关系？（由于电子的速度很大，交变电压周期较大，同一电子穿过电场的过程可认为电场没有变化，是稳定的匀强电场）
【答案】(1)
(2)
(3)
,
【解析】
因为粒子在磁场中运动洛伦兹力不做功，所以根据动能定理求出电子射出加速电场时的速度大小，即为电子束经偏转磁场后打到荧光屏上时的速率；粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，出磁场后做匀速直线运动，通过最大的偏转角，结合几何关系求出荧光屏上亮线的长度；类平抛运动利用运动的合成和分解，结合电场中牛顿第二定律，根据速度偏向角的几何关系，联立即可求出极板间正弦交变电压的最大值Um，极板长度L、极板间距离d之间需要满足的关系式；
解：(1)设经过电子枪中加速电场加速后，电子的速度大小为v
根据动能定理可得：
电子束经过磁场区域速度大小不变，电子束打在荧光屏上速率为：
(2)设电子在磁场中做圆周运动的半径为R，运动轨迹如图所示
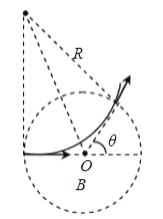
根据几何关系有：
洛伦兹力提供向心力，根据牛顿第二定律有：
当
时，电子束经过磁场偏转角为θ，此时电子在荧光屏上的落点距M点最远，解得：
电子在荧光屏上落点距M点最远距离：
荧光屏上亮线长度：
(3)若使电子束打在荧光屏上所形成亮线的长度与磁场中偏转时相同，则电子束的最大偏转角
保持不变，即：
当电子达到最大偏转角时，恰好从极板边缘射出。
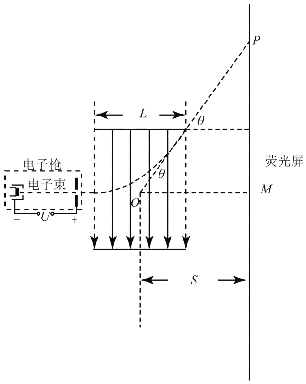
这种情况下，
，即：
设此时两极板间电压为U1
由牛顿第二定律有：
由匀加速直线运动规律有：
且：
联立解得：
当极板间电压再大时，电子不能从极板边界射出，故不会形成亮线，因此：
当电子达到最大偏转角时，不是从极板边界射出，即：
，此时两极板间电压达到Um(电压再增大，电子偏转角增加，亮线长度增加)
由牛顿第二定律有：
由匀加速直线运动规律有：
，
联立解得：
