题目内容
5. 如图所示,MN为水平地面,A、B物块与O点左侧地面的滑动摩檫因素为μ,右侧是光滑的,一轻质弹簧右端固定在墙壁上,左端与静止在O点、质量为 m的小物块A连接,弹簧处于原长状态. 质量为2m的物块B静止在C处,受到水平瞬时冲量作用后获得向右的速度v0,物块B运动到O点与物块A相碰后一起向右运动,碰撞不粘连(设碰撞时间极短),不计空气阻力.CO=5L,物块B和物块A均可视为质点.求物块B最终停止的位置离O点多远?
如图所示,MN为水平地面,A、B物块与O点左侧地面的滑动摩檫因素为μ,右侧是光滑的,一轻质弹簧右端固定在墙壁上,左端与静止在O点、质量为 m的小物块A连接,弹簧处于原长状态. 质量为2m的物块B静止在C处,受到水平瞬时冲量作用后获得向右的速度v0,物块B运动到O点与物块A相碰后一起向右运动,碰撞不粘连(设碰撞时间极短),不计空气阻力.CO=5L,物块B和物块A均可视为质点.求物块B最终停止的位置离O点多远?
分析 对CO过程由动能定理可求得物体B到达O处时的速度表达式;再对碰撞过程由动量守恒定律可知碰后的速度;再对B在CO过程由动能定理可求得物块B最终的位置.
解答 解:设B到达O处时速度为VB,对B由动能定理得:
-μ•2mg•5L=$\frac{1}{2}$m$V_B^2$-$\frac{1}{2}$m$V_O^2$…①
设BA碰后速度为V,碰撞中,设向右为正方向,由动量守恒定律得:
2mVB=3mV…②
AB相碰到回到O处的过程中,由机械能守恒可知AB返回向左运动到O处分离时,B的速度仍为V,设B离O的最远距离为SB,对B又由动能定理得:
μ×2mgSB=$\frac{1}{2}$Mv2 …③
解①②③得:
SB=$\frac{2({v}_{0}^{2}-10μgL)}{9μg}$
答:物块B最终停止的位置离O点$\frac{2({v}_{0}^{2}-10μgL)}{9μg}$.
点评 本题考查动量守恒定律及功能关系的应用,要认真分析物体的运动过程,对每一过程分析受力情况,由动量守恒定律结合功能关系进行分析即可.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
15.火车轨道在转弯处外轨高于内轨,其高度差由转弯半径与火车速度确定.若在某转弯处规定行驶的速度为v,则下列说法中正确的是( )
| A. | 当以v的速度通过此弯路时,火车重力、轨道面支持力和摩擦力的合力提供向心力 | |
| B. | 当以v的速度通过此弯路时,火车重力、轨道面支持力和外轨对轮缘弹力的合力提供向心力 | |
| C. | 当速度大于v时,火车轮缘挤压外轨 | |
| D. | 当速度小于v时,火车轮缘挤压外轨 |
16. 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.xOy平面的第一象限,存在以x轴、y轴及双曲线y=$\frac{{L}^{2}}{4x}$的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ(即ABCOD区域);在第二象限存在以x=-L、x=-2L、y=0、y=L为边界的匀强电场区域Ⅱ(即正方形MNPQ区域).两个电场强度的大小均为E,电子的电荷量为e,不计电子重力的影响,则从电场Ⅰ区域的AB曲线边界由静止释放的各个电子( )
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.xOy平面的第一象限,存在以x轴、y轴及双曲线y=$\frac{{L}^{2}}{4x}$的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ(即ABCOD区域);在第二象限存在以x=-L、x=-2L、y=0、y=L为边界的匀强电场区域Ⅱ(即正方形MNPQ区域).两个电场强度的大小均为E,电子的电荷量为e,不计电子重力的影响,则从电场Ⅰ区域的AB曲线边界由静止释放的各个电子( )
 如图所示为研究电子枪中电子在电场中运动的简化模型示意图.xOy平面的第一象限,存在以x轴、y轴及双曲线y=$\frac{{L}^{2}}{4x}$的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ(即ABCOD区域);在第二象限存在以x=-L、x=-2L、y=0、y=L为边界的匀强电场区域Ⅱ(即正方形MNPQ区域).两个电场强度的大小均为E,电子的电荷量为e,不计电子重力的影响,则从电场Ⅰ区域的AB曲线边界由静止释放的各个电子( )
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.xOy平面的第一象限,存在以x轴、y轴及双曲线y=$\frac{{L}^{2}}{4x}$的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ(即ABCOD区域);在第二象限存在以x=-L、x=-2L、y=0、y=L为边界的匀强电场区域Ⅱ(即正方形MNPQ区域).两个电场强度的大小均为E,电子的电荷量为e,不计电子重力的影响,则从电场Ⅰ区域的AB曲线边界由静止释放的各个电子( )| A. | 在电场区域Ⅱ中运动时间不相同 | |
| B. | 全部从同一位置处离开区域Ⅱ | |
| C. | 从PN间和PQ间不同位置处离开区域Ⅱ | |
| D. | 离开MNPQ的最小动能为eEL |
13.图乙中,理想变压器原、副线圈匝数比n1:n2=5:1.原线圈接入如图甲所示的正弦交流电.电路中电表均为理想电表,定值电阻R1=R2=4Ω,D为理想二极管(该二极管的正向电阻为零,反向电阻为无穷大),则( )


| A. | 电阻R2两端的电压频率为50Hz | B. | 电流表的示数为5A | ||
| C. | 原线圈的输入功率为150W | D. | 将R1摘掉,电压表的示数不变 |
20. 如图所示,一束由两种色光混合的复色光沿PO方向射向一厚玻璃平面镜的上表面,出射光分成Ⅰ、Ⅱ两束单色光,则下列说法正确的是( )
如图所示,一束由两种色光混合的复色光沿PO方向射向一厚玻璃平面镜的上表面,出射光分成Ⅰ、Ⅱ两束单色光,则下列说法正确的是( )
 如图所示,一束由两种色光混合的复色光沿PO方向射向一厚玻璃平面镜的上表面,出射光分成Ⅰ、Ⅱ两束单色光,则下列说法正确的是( )
如图所示,一束由两种色光混合的复色光沿PO方向射向一厚玻璃平面镜的上表面,出射光分成Ⅰ、Ⅱ两束单色光,则下列说法正确的是( )| A. | Ⅰ、Ⅱ两束反射光一定相互平行 | |
| B. | 玻璃对Ⅰ光的折射率大于Ⅱ光的折射率 | |
| C. | Ⅰ光光子的能量小于Ⅱ光光子的能量 | |
| D. | Ⅰ光在玻璃中的波长小于Ⅱ光在玻璃中的波长 |
10. 如图所示,斜面体固定在水平地面上.一物体在沿斜面向上且平行斜面的力F1作用下,在斜面上做速度为v1的匀速运动,F1的功率为P0.若该物体在沿斜面斜向上的且与斜面夹角为α的力F2(如图)作用下,在同一斜面上做速度为v2的匀速运动,F2的功率也为P0,则下列说法中正确的是( )
如图所示,斜面体固定在水平地面上.一物体在沿斜面向上且平行斜面的力F1作用下,在斜面上做速度为v1的匀速运动,F1的功率为P0.若该物体在沿斜面斜向上的且与斜面夹角为α的力F2(如图)作用下,在同一斜面上做速度为v2的匀速运动,F2的功率也为P0,则下列说法中正确的是( )
 如图所示,斜面体固定在水平地面上.一物体在沿斜面向上且平行斜面的力F1作用下,在斜面上做速度为v1的匀速运动,F1的功率为P0.若该物体在沿斜面斜向上的且与斜面夹角为α的力F2(如图)作用下,在同一斜面上做速度为v2的匀速运动,F2的功率也为P0,则下列说法中正确的是( )
如图所示,斜面体固定在水平地面上.一物体在沿斜面向上且平行斜面的力F1作用下,在斜面上做速度为v1的匀速运动,F1的功率为P0.若该物体在沿斜面斜向上的且与斜面夹角为α的力F2(如图)作用下,在同一斜面上做速度为v2的匀速运动,F2的功率也为P0,则下列说法中正确的是( )| A. | F2大于F1 | |
| B. | 在相同的时间内,物体增加的机械能相同 | |
| C. | v1一定小于v2 | |
| D. | v1可能小于v2 |
17.下列说法中正确的有( )
| A. | 不管光源与观察者是否存在相对运动,观察者观察到的光速是不变的 | |
| B. | 水面上的油膜呈现彩色是光的干涉现象 | |
| C. | 在光导纤维束内传送图象是利用光的色散现象 | |
| D. | 声源向静止的观察者运动,观察者接收到的频率小于声源的频率 |
14. 如图所示,a、b两束不同频率的单色光以45°的入射角射到玻璃砖的上表面上,入射点分别为A、B.直线OO′垂直玻璃砖与玻璃砖上表面相交于E点.A、B到E的距离相等.a、b两束光与直线OO′在同一平面内(图中纸面内).经过玻璃砖后,a、b两束光相交于图中的P点.则下列判断中正确的是( )
如图所示,a、b两束不同频率的单色光以45°的入射角射到玻璃砖的上表面上,入射点分别为A、B.直线OO′垂直玻璃砖与玻璃砖上表面相交于E点.A、B到E的距离相等.a、b两束光与直线OO′在同一平面内(图中纸面内).经过玻璃砖后,a、b两束光相交于图中的P点.则下列判断中正确的是( )
 如图所示,a、b两束不同频率的单色光以45°的入射角射到玻璃砖的上表面上,入射点分别为A、B.直线OO′垂直玻璃砖与玻璃砖上表面相交于E点.A、B到E的距离相等.a、b两束光与直线OO′在同一平面内(图中纸面内).经过玻璃砖后,a、b两束光相交于图中的P点.则下列判断中正确的是( )
如图所示,a、b两束不同频率的单色光以45°的入射角射到玻璃砖的上表面上,入射点分别为A、B.直线OO′垂直玻璃砖与玻璃砖上表面相交于E点.A、B到E的距离相等.a、b两束光与直线OO′在同一平面内(图中纸面内).经过玻璃砖后,a、b两束光相交于图中的P点.则下列判断中正确的是( )| A. | 在真空中,a光的传播速度大于b光的传播速度 | |
| B. | 在玻璃中,a光的传播速度小于b光的传播速度 | |
| C. | 同时增大入射角,则b光的出射光线先消失 | |
| D. | 对同一双缝干涉装置,a光的干涉条纹比b光的干涉条纹宽 |
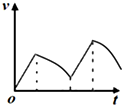
 如图所示,两根电阻不计的光滑金属导轨竖直放置,导轨上端接有电阻R,水平条形区域I和Ⅱ内有相同的方向垂直轨道平面向里的匀强磁场,I和Ⅱ之间无磁场.一电阻不计的导体棒,两端与导轨保持良好接触.现将导体棒由区域I上边界H处静止释放,并穿过两磁场区域,图中能定性描述该过程导体棒速度与时间关系的图象可能是( )
如图所示,两根电阻不计的光滑金属导轨竖直放置,导轨上端接有电阻R,水平条形区域I和Ⅱ内有相同的方向垂直轨道平面向里的匀强磁场,I和Ⅱ之间无磁场.一电阻不计的导体棒,两端与导轨保持良好接触.现将导体棒由区域I上边界H处静止释放,并穿过两磁场区域,图中能定性描述该过程导体棒速度与时间关系的图象可能是( )