Question

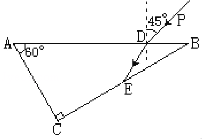
【题目】如图所示，直角三角形ABC是一玻璃砖的横截面，AB=L，∠C=90°，∠A=60°．一束单色光PD从AB边上的D点射入玻璃砖，入射角为45°，DB=L/4，折射光DE恰好射到玻璃砖BC边的中点E，已知光在真空中的传播速度为c．求：

①．玻璃砖的折射率；

②．该光束从AB边上的D点射入玻璃砖到第一次射出玻璃砖所需的时间．

Answer 1

【答案】（1） （2）

【解析】①．作出光路图，如图所示

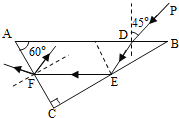
过E点的法线是三角形的中位线，由几何关系可知△DEB为等腰三角形，DE=DB=

由几何知识可知光在AB边折射时折射角为 r=30°，
所以玻璃砖的折射率为
②．设临界角为θ，有sinθ=，可解得 θ=45°
由光路图及几何知识可判断，光在BC边上的入射角为60°，大于临界角，则光在BC边上发生全反射；光在AC边的入射角为30°，小于临界角，所以光从AC第一次射出玻璃砖，
根据几何知识可知 EF=, 则光束从AB边射入玻璃砖到第一次射出玻璃砖所需要的时间为
而 ，可解得：

解决本题关键是作出光路图，再运用几何知识求解入射角折射角，要掌握几何光学常用的三个规律：折射定律 、临界角公式sinC=和光速公式．