题目内容
【题目】如图,一质量m2=0.25kg的平顶小车,车顶右端放一质量m3=0.2kg的小物体,小物体可视为质点,与车顶之间的动摩擦因数μ=0.4,小车静止在光滑的水平轨道上.现有一质量m1=0.05kg的子弹以水平速度v0=12m/s射中小车左端,并留在车中.子弹与车相互作用时间很短.若使小物体不从车顶上滑落,g取10m/s2 . 求: 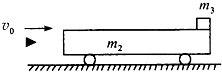
(1)最后物体与车的共同速度为多少?小车的最小长度应为多少?
(2)小木块在小车上滑行的时间.
【答案】
(1)解:子弹进入小车的过程中,子弹与小车组成的系统动量守恒,以子弹速度初速度方向为正方向,由动量守恒定律得:
m1v0=(m2+m1)v1①
由三物体组成的系统动量守恒,以子弹速度初速度方向为正方向,由动量守恒定律得:
(m2+m1)v1=(m2+m1+m3)v2②
设小车最小长度为L,三物体相对静止后,对系统利用能量守恒定律得:
![]() (m2+m1)v12﹣
(m2+m1)v12﹣ ![]() (m2+m1+m3)
(m2+m1+m3) ![]() =μm3gL③
=μm3gL③
联立以上方程解得:L=0.3m
车与物体的共同速度为:v2=1.2m/s
(2)解:以m3为研究对象,利用动量定理可得:μm3gt=m3v2
解得:t=0.3s
【解析】(1、2)子弹进入小车的过程中,子弹与小车组成的系统动量守恒,由动量守恒定律列式,三物体组成的系统动量守恒,由动量守恒定律列式,设小车最小长度为L,三物体相对静止后,对系统利用能量守恒定律列式,联立方程即可求解;(3)以m3为研究对象,利用动量定理列式即可求解.
【考点精析】掌握动量守恒定律是解答本题的根本,需要知道动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.

 阅读快车系列答案
阅读快车系列答案