题目内容
 如图所示,一带电量为-q、质量为m的粒子以初速度v0从两平行板电容器中央水平射入,从离上板为
如图所示,一带电量为-q、质量为m的粒子以初速度v0从两平行板电容器中央水平射入,从离上板为| 1 | 4 |
(1)两板所加电压多大?
(2)飞离平行板时带电粒子速度多大?
分析:(1)粒子在两板在做类平抛运动,根据水平位移和初速度求出运动的时间,结合牛顿第二定律和运动学公式求出两板间所加的电压.
(2)根据动能定理求出飞离平行板时带电粒子速度.
(2)根据动能定理求出飞离平行板时带电粒子速度.
解答:解:(1)因为偏转位移y=
.
根据y=
at2,l=v0t
又qE=ma,E=
联立解得U=
.
(2)根据动能定理得,
q=
mv2-
mv02
解得v=v0
.
答:(1)两板所加电压U=
.
(2)飞离平行板时带电粒子速度v=v0
.
| d |
| 4 |
根据y=
| 1 |
| 2 |
又qE=ma,E=
| U |
| d |
联立解得U=
| md2v02 |
| 2qL2 |
(2)根据动能定理得,
| U |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解得v=v0
|
答:(1)两板所加电压U=
| md2v02 |
| 2qL2 |
(2)飞离平行板时带电粒子速度v=v0
|
点评:带电粒子垂直电场射入,做类平抛运动,常用的处理方法是分解,结合沿电场方向和垂直电场方向上的运动规律,通过牛顿第二定律和运动学公式进行求解.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图所示,一带电量为q的金属球,固定在绝缘的支架上,这时球外P点的电场强度为E0,当把一电量也是q的点电荷放在P点时,测得点电荷受到的静电力为f;当把一电量为aq的点电荷放在P点时,测得作用于这点电荷的静电力为F,则在国际单位制中( )
如图所示,一带电量为q的金属球,固定在绝缘的支架上,这时球外P点的电场强度为E0,当把一电量也是q的点电荷放在P点时,测得点电荷受到的静电力为f;当把一电量为aq的点电荷放在P点时,测得作用于这点电荷的静电力为F,则在国际单位制中( ) 如图所示,一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d,+q到带电薄板的垂线通过板的几何中心,若图中a点处的合电场强度为零,正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为(静电力恒量为k)( )
如图所示,一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d,+q到带电薄板的垂线通过板的几何中心,若图中a点处的合电场强度为零,正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为(静电力恒量为k)( ) 如图所示,一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d,+q到带电薄板的垂线通过板的几何中心,若图中a点处的合电场强度为零,正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为(静电力恒量为k)( )
如图所示,一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d,+q到带电薄板的垂线通过板的几何中心,若图中a点处的合电场强度为零,正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为(静电力恒量为k)( )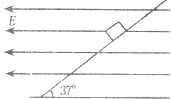 如图所示,一带电量为q、质量为m的小物块处于一倾角为37°的光滑面上,当整个装置处于一水平向左的匀强电场中时,小物块恰好处于静止状态.某时刻,电场强度突然减小为原来的
如图所示,一带电量为q、质量为m的小物块处于一倾角为37°的光滑面上,当整个装置处于一水平向左的匀强电场中时,小物块恰好处于静止状态.某时刻,电场强度突然减小为原来的