题目内容
如图所示，一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d，+q到带电薄板的垂线通过板的几何中心，若图中a点处的合电场强度为零，正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为（静电力恒量为k）（ ）分析：据题，a点处的电场强度为零，+q与带电薄板在a点产生的场强大小相等，方向相反．+q在a处产生的场强大小为E=
，得到带电薄板在a点产生的场强大小，根据对称性，确定带电薄板在b点产生的场强大小．+q在b处产生的场强大小为E=k
，再根据叠加原理求解b点处的电场强度大小．
| kQ |
| r2 |
| q |
| (3d)2 |
解答：解：+q在a处产生的场强大小为E=k
，方向水平向左．据题，a点处的电场强度为零，+q与带电薄板在a点产生的场强大小相等，方向相反，则带电薄板在a点产生的场强大小为E=k
，方向水平向右．根据对称性可知，带电薄板在b点产生的场强大小为E=
，方向水平向左．+q在b处产生的场强大小为E=k
，方向水平向左，则b点处的电场强度大小是Eb=
．
故选A．
| kq |
| d2 |
| kq |
| d2 |
| kq |
| d2 |
| q |
| (3d)2 |
| 10kq |
| 9d2 |
故选A．
点评：本题考查电场的叠加，关键要抓住带电薄板产生的电场的对称性．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，一带电量为q的金属球，固定在绝缘的支架上，这时球外P点的电场强度为E0，当把一电量也是q的点电荷放在P点时，测得点电荷受到的静电力为f；当把一电量为aq的点电荷放在P点时，测得作用于这点电荷的静电力为F，则在国际单位制中（ ）
如图所示，一带电量为-q、质量为m的粒子以初速度v0从两平行板电容器中央水平射入，从离上板为
如图所示，一带电量为+q的点电荷与均匀带电的正三角形的薄板相距为2d，+q到带电薄板的垂线通过板的几何中心，若图中a点处的合电场强度为零，正确应用等效和对称的思维方法求出带电薄板与+q在图中b点处产生的合电场强度大小为（静电力恒量为k）（ ）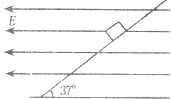
如图所示，一带电量为q、质量为m的小物块处于一倾角为37°的光滑面上，当整个装置处于一水平向左的匀强电场中时，小物块恰好处于静止状态．某时刻，电场强度突然减小为原来的