题目内容
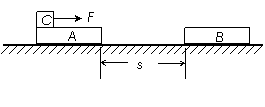
如图所示,两个相同的木板A、B置于水平地面上,质量均为m=1kg,其中B固定不动,A可以沿地面滑动,它们相距s=1.5m。质量为2m,大小可忽略的物块C置于A板的左端。C与A之间的动摩擦因数为μ1=0.22,A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可以认为等于滑动摩擦力。现给C施加一个水平向右,大小为0.4mg的水平恒力F,使其开始运动,设A与B发生碰撞后立即静止,重力加速度g=10m/s2。求
(1)要使C最终不脱离木板,每块木板的长度至少应为多少?
(2)若C恰好没有脱离木板,水平恒力F所做的功。
答案:(1)1.25 m;(2)16J
解析:(1)由于C与木板间的滑动摩擦力f1=μ1×2mg=0.44 mg> F=0.4 mg,
所以,A和C能保持相对静止。(2分)
在F的作用下一起向右匀加速运动,设A刚要与B发生碰撞时的速度为v,对AC整体,由动能定理得
(F-3μ2mg)s=![]() ,(3分)
,(3分)
解得v=1 m/s 。(1分)
A与B发生碰撞后停止,C在木板上做匀减速直线运动,若刚好滑到B的最右端恰好停止,则木板的长度最小。对C物体,由动能定理得
(F-μ1×2mg)![]() =
=![]() ,(2分)
,(2分)
解得L=1.25 m,即每块木板的长度至少应为1.25 m。(1分)
(2)C恰好没有脱离木板,C的位移为![]() m,(3分)
m,(3分)
故水平恒力F所做的功为![]() J。(2分)
J。(2分)

练习册系列答案
相关题目
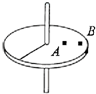 如图所示,两个相同的物块A、B(可视为质点),放在不光滑的水平旋转台上,A离轴距离为r,B离轴距离为2r,则圆台旋转时,下列说法正确的是( )
如图所示,两个相同的物块A、B(可视为质点),放在不光滑的水平旋转台上,A离轴距离为r,B离轴距离为2r,则圆台旋转时,下列说法正确的是( )| A、当A、B都未滑动时,A受到的静摩擦力大于B受到的静摩擦力 | B、当A、B都未滑动时,B受到的静摩擦力大于A受到的静摩擦力 | C、若圆台转速逐渐增大,则A先做离心运动 | D、若圆台转速逐渐增大,则B先做离心运动 |
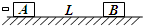 如图所示,两个相同的木块A、B静止在水平面上,它们之间的距离为L,今有一颗子弹以较大的速度依次射穿了A、B,在子弹射出A时,A的速度为vA,子弹穿出B时,B的速度为vB,A、B停止时,它们之间的距离为s,整个过程A、B没有相碰,则( )
如图所示,两个相同的木块A、B静止在水平面上,它们之间的距离为L,今有一颗子弹以较大的速度依次射穿了A、B,在子弹射出A时,A的速度为vA,子弹穿出B时,B的速度为vB,A、B停止时,它们之间的距离为s,整个过程A、B没有相碰,则( ) 如图所示,两个相同的灯泡A、B分别接在理想变压器的原、副线圈上(灯泡的电阻不随温度变化),已知原、副线圈的匝数比n1:n2=2:1,电源的电压为U,则( )
如图所示,两个相同的灯泡A、B分别接在理想变压器的原、副线圈上(灯泡的电阻不随温度变化),已知原、副线圈的匝数比n1:n2=2:1,电源的电压为U,则( )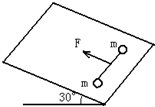 如图所示,两个相同的质量m=0.2kg的小球用长L=0.22m的细绳连接,放在倾角为30°的光滑斜面上.初始时刻,细绳拉直,且绳与斜面底边平行.在绳的中点作用一个垂直于绳沿斜面向上的恒力F=2.2N.在F的作用下两小球向上运动,小球沿F方向的位移随时间变化的关系式为s=kt2(k为恒量).经过一段时间两个小球第一次碰撞,又经过一段时间再一次发生碰撞….由于两小球之间有粘性,每一次碰撞后,小球垂直于F方向的速度将损失0.3m/s.当力F作用了2s时,两小球发生最后一次碰撞,且不再分开.取g=10m/s2,求:
如图所示,两个相同的质量m=0.2kg的小球用长L=0.22m的细绳连接,放在倾角为30°的光滑斜面上.初始时刻,细绳拉直,且绳与斜面底边平行.在绳的中点作用一个垂直于绳沿斜面向上的恒力F=2.2N.在F的作用下两小球向上运动,小球沿F方向的位移随时间变化的关系式为s=kt2(k为恒量).经过一段时间两个小球第一次碰撞,又经过一段时间再一次发生碰撞….由于两小球之间有粘性,每一次碰撞后,小球垂直于F方向的速度将损失0.3m/s.当力F作用了2s时,两小球发生最后一次碰撞,且不再分开.取g=10m/s2,求: 如图所示,两个相同的弧形轨道M、N,分别用于发射小铁球P、Q,其中N的末端可看作与光滑的水平板相切,两轨道上端分别装有电磁铁C、D,调节电磁铁C、D的高度使AC=BD,从而保证小铁球P、Q在轨道出口处的水平速度相等.现将小铁球P、Q分别吸于电磁铁C、D上,然后切断电源,使两小球能以相同的速度同时分别从轨道M、N的下端射出.
如图所示,两个相同的弧形轨道M、N,分别用于发射小铁球P、Q,其中N的末端可看作与光滑的水平板相切,两轨道上端分别装有电磁铁C、D,调节电磁铁C、D的高度使AC=BD,从而保证小铁球P、Q在轨道出口处的水平速度相等.现将小铁球P、Q分别吸于电磁铁C、D上,然后切断电源,使两小球能以相同的速度同时分别从轨道M、N的下端射出.