题目内容
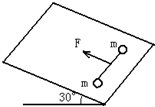 如图所示,两个相同的质量m=0.2kg的小球用长L=0.22m的细绳连接,放在倾角为30°的光滑斜面上.初始时刻,细绳拉直,且绳与斜面底边平行.在绳的中点作用一个垂直于绳沿斜面向上的恒力F=2.2N.在F的作用下两小球向上运动,小球沿F方向的位移随时间变化的关系式为s=kt2(k为恒量).经过一段时间两个小球第一次碰撞,又经过一段时间再一次发生碰撞….由于两小球之间有粘性,每一次碰撞后,小球垂直于F方向的速度将损失0.3m/s.当力F作用了2s时,两小球发生最后一次碰撞,且不再分开.取g=10m/s2,求:
如图所示,两个相同的质量m=0.2kg的小球用长L=0.22m的细绳连接,放在倾角为30°的光滑斜面上.初始时刻,细绳拉直,且绳与斜面底边平行.在绳的中点作用一个垂直于绳沿斜面向上的恒力F=2.2N.在F的作用下两小球向上运动,小球沿F方向的位移随时间变化的关系式为s=kt2(k为恒量).经过一段时间两个小球第一次碰撞,又经过一段时间再一次发生碰撞….由于两小球之间有粘性,每一次碰撞后,小球垂直于F方向的速度将损失0.3m/s.当力F作用了2s时,两小球发生最后一次碰撞,且不再分开.取g=10m/s2,求:(1)最后一次碰撞后,小球的加速度
(2)最后一次碰撞后瞬间,小球的速度
(3)整个碰撞过程中,系统损失的机械能
(4)两小球相碰的总次数.
分析:(1)小球发生最后一次碰撞,不再分开,加速度相同,将两个小球看成整体,根据牛顿第二定律求加速度a.
(2)最后一次碰撞结束时,两小球粘合成一个整体,由运动学公式求解最后一次碰撞结束时小球的速度;
(3)整个碰撞过程中,F做功为F(
+
at2),转化为两小球的动能和内能,根据功能关系列式求解;
(4)根据功能关系求第一次碰撞前,两球在水平、竖直两个方向的分速度vx和vy.根据条件:每一次碰撞后,小球垂直于F方向的速度将减小0.55m/s,即可求出碰撞的次数.
(2)最后一次碰撞结束时,两小球粘合成一个整体,由运动学公式求解最后一次碰撞结束时小球的速度;
(3)整个碰撞过程中,F做功为F(
| L |
| 2 |
| 1 |
| 2 |
(4)根据功能关系求第一次碰撞前,两球在水平、竖直两个方向的分速度vx和vy.根据条件:每一次碰撞后,小球垂直于F方向的速度将减小0.55m/s,即可求出碰撞的次数.
解答:解:(1)对两小球组成的整体分析,由牛顿第二定律有 a=
=0.5m/s2…①
(2)∵小球沿F方向的位移随时间变化的关系式为S=kt2(k为恒量)
∴是匀加速运动vt=at=0.5×2m/s=1m/s…②
(3)根据功能原理:△E=F(s+
)-2mgSin30°?s+
?2mvt2…③
F(
at2+
)-2mSin30°?
at2+
?2mvt2=0.242J
(4)假设在拉力作用的前2s内两球未发生碰撞,在2s时,小球沿F方向的分速度为vx,垂直于F方向的分速度为vy
根据动能定理:F(s+
)=2mgSin30°?s+
?2mvx2+
?2mvy2…④
vx=at…⑤
s=
at2…⑥
解④、⑤、⑥得:vy=1.1m/s
∵每次碰撞后小球垂直于F方向的速度将损失0.3m/s
∴n=
=3.67(次)≈4次
答:
(1)最后一次碰撞后,小球的加速度为0.5m/s2.
(2)最后一次碰撞后瞬间,小球的速度是1m/s.
(3)整个碰撞过程中,系统损失的机械能是0.242J.
(4)两小球相碰的总次数是4次.
| F-2mgsin30° |
| 2m |
(2)∵小球沿F方向的位移随时间变化的关系式为S=kt2(k为恒量)
∴是匀加速运动vt=at=0.5×2m/s=1m/s…②
(3)根据功能原理:△E=F(s+
| L |
| 2 |
| 1 |
| 2 |
F(
| 1 |
| 2 |
| L |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(4)假设在拉力作用的前2s内两球未发生碰撞,在2s时,小球沿F方向的分速度为vx,垂直于F方向的分速度为vy
根据动能定理:F(s+
| L |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
vx=at…⑤
s=
| 1 |
| 2 |
解④、⑤、⑥得:vy=1.1m/s
∵每次碰撞后小球垂直于F方向的速度将损失0.3m/s
∴n=
| 1.1 |
| 0.3 |
答:
(1)最后一次碰撞后,小球的加速度为0.5m/s2.
(2)最后一次碰撞后瞬间,小球的速度是1m/s.
(3)整个碰撞过程中,系统损失的机械能是0.242J.
(4)两小球相碰的总次数是4次.
点评:本题关键采用整体法求水平方向的加速度,运用功能关系和运动学公式结合求碰前两个球的分速度.

练习册系列答案
相关题目
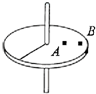 如图所示,两个相同的物块A、B(可视为质点),放在不光滑的水平旋转台上,A离轴距离为r,B离轴距离为2r,则圆台旋转时,下列说法正确的是( )
如图所示,两个相同的物块A、B(可视为质点),放在不光滑的水平旋转台上,A离轴距离为r,B离轴距离为2r,则圆台旋转时,下列说法正确的是( )| A、当A、B都未滑动时,A受到的静摩擦力大于B受到的静摩擦力 | B、当A、B都未滑动时,B受到的静摩擦力大于A受到的静摩擦力 | C、若圆台转速逐渐增大,则A先做离心运动 | D、若圆台转速逐渐增大,则B先做离心运动 |
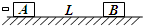 如图所示,两个相同的木块A、B静止在水平面上,它们之间的距离为L,今有一颗子弹以较大的速度依次射穿了A、B,在子弹射出A时,A的速度为vA,子弹穿出B时,B的速度为vB,A、B停止时,它们之间的距离为s,整个过程A、B没有相碰,则( )
如图所示,两个相同的木块A、B静止在水平面上,它们之间的距离为L,今有一颗子弹以较大的速度依次射穿了A、B,在子弹射出A时,A的速度为vA,子弹穿出B时,B的速度为vB,A、B停止时,它们之间的距离为s,整个过程A、B没有相碰,则( ) 如图所示,两个相同的灯泡A、B分别接在理想变压器的原、副线圈上(灯泡的电阻不随温度变化),已知原、副线圈的匝数比n1:n2=2:1,电源的电压为U,则( )
如图所示,两个相同的灯泡A、B分别接在理想变压器的原、副线圈上(灯泡的电阻不随温度变化),已知原、副线圈的匝数比n1:n2=2:1,电源的电压为U,则( ) 如图所示,两个相同的弧形轨道M、N,分别用于发射小铁球P、Q,其中N的末端可看作与光滑的水平板相切,两轨道上端分别装有电磁铁C、D,调节电磁铁C、D的高度使AC=BD,从而保证小铁球P、Q在轨道出口处的水平速度相等.现将小铁球P、Q分别吸于电磁铁C、D上,然后切断电源,使两小球能以相同的速度同时分别从轨道M、N的下端射出.
如图所示,两个相同的弧形轨道M、N,分别用于发射小铁球P、Q,其中N的末端可看作与光滑的水平板相切,两轨道上端分别装有电磁铁C、D,调节电磁铁C、D的高度使AC=BD,从而保证小铁球P、Q在轨道出口处的水平速度相等.现将小铁球P、Q分别吸于电磁铁C、D上,然后切断电源,使两小球能以相同的速度同时分别从轨道M、N的下端射出.