题目内容
19.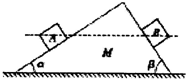 如图所示,一个顶角为90°的斜面体M置于水平面上,它的底面粗糙,两斜面光滑,两个斜面与水平面的夹角分别为α、β,且α<β,将质量相等的A、B两个小滑块同时从斜面上同一高度处静止释放,在两滑块滑至斜面底端的过程中,M始终保持静止.则( )
如图所示,一个顶角为90°的斜面体M置于水平面上,它的底面粗糙,两斜面光滑,两个斜面与水平面的夹角分别为α、β,且α<β,将质量相等的A、B两个小滑块同时从斜面上同一高度处静止释放,在两滑块滑至斜面底端的过程中,M始终保持静止.则( )| A. | 地面对斜面体的支持力小于三个物体的总重力 | |
| B. | 两滑块滑至斜面底端所用的时间相同 | |
| C. | 两滑块滑至斜面底端时重力的瞬时功率相同 | |
| D. | 地面对斜面体的支持力等于三个物体的总重力 |
分析 根据牛顿第二定律求出物块下滑的加速度,根据位移时间公式求出运动的时间,从而比较运动时间的长短,根据速度时间公式求出滑块到达底端的速度,从而求出重力的瞬时功率.对M分析,根据共点力平衡分析地面对斜面体是否有摩擦力,对整体分析,根据A、B加速度的方向确定整体处于超重还是失重.
解答 解:A、D、因为A、B的加速度均沿斜面向下,对整体分析,整体处于失重状态,则支持力小于三个物体的总重力.故A正确,D错误;
B、物块A下滑的加速度a=gsinα,位移x=$\frac{h}{sinα}$,根据x=$\frac{1}{2}a{t}^{2}$得,t=$\frac{1}{sinα}\sqrt{\frac{2h}{g}}$,同理,B下滑的时间t=$\frac{1}{sinβ}\sqrt{\frac{2h}{g}}$,可知两滑块滑至底端的时间不同.故B错误.
C、物块A滑到底端的速度v=$at=\sqrt{2gh}$,B滑到底端的速度也为$\sqrt{2gh}$,由于两物体的速度方向不同,则重力的瞬时功率不同.故C错误.
故选:A.
点评 本题综合考查了牛顿第二定律和运动学公式,综合性较强,注意瞬时功率P=mgcosθ,θ为力与速度的夹角.

练习册系列答案
相关题目
1.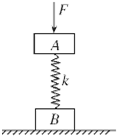 如图所示,质量分别为mA=2kg和mB=3kg的A?B两物块,用劲度系数为k的轻弹簧相连后竖直放在水平面上,今用大小为F=45N的力把物块A向下压而使之处于静止,突然撤去压力,则( )
如图所示,质量分别为mA=2kg和mB=3kg的A?B两物块,用劲度系数为k的轻弹簧相连后竖直放在水平面上,今用大小为F=45N的力把物块A向下压而使之处于静止,突然撤去压力,则( )
 如图所示,质量分别为mA=2kg和mB=3kg的A?B两物块,用劲度系数为k的轻弹簧相连后竖直放在水平面上,今用大小为F=45N的力把物块A向下压而使之处于静止,突然撤去压力,则( )
如图所示,质量分别为mA=2kg和mB=3kg的A?B两物块,用劲度系数为k的轻弹簧相连后竖直放在水平面上,今用大小为F=45N的力把物块A向下压而使之处于静止,突然撤去压力,则( )| A. | 物块A振动的平衡位置处时弹簧弹力为0 | |
| B. | 物块B不可能离开水平面 | |
| C. | 只要k足够小,物块B就可能离开水平面 | |
| D. | 只要k足够大,物块B就可能离开水平面 |
10.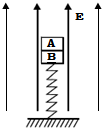 如图所示,质量均为m的A、B两物体叠放在竖直轻质弹簧上并保持静止,其中A带正电,电荷量大小为q,B始终不带电.现在A、B所在空间加上竖直向上的匀强电场,A、B开始向上运动,从开始运动到A和B刚好分离的过程中,下列说法正确的是( )
如图所示,质量均为m的A、B两物体叠放在竖直轻质弹簧上并保持静止,其中A带正电,电荷量大小为q,B始终不带电.现在A、B所在空间加上竖直向上的匀强电场,A、B开始向上运动,从开始运动到A和B刚好分离的过程中,下列说法正确的是( )
 如图所示,质量均为m的A、B两物体叠放在竖直轻质弹簧上并保持静止,其中A带正电,电荷量大小为q,B始终不带电.现在A、B所在空间加上竖直向上的匀强电场,A、B开始向上运动,从开始运动到A和B刚好分离的过程中,下列说法正确的是( )
如图所示,质量均为m的A、B两物体叠放在竖直轻质弹簧上并保持静止,其中A带正电,电荷量大小为q,B始终不带电.现在A、B所在空间加上竖直向上的匀强电场,A、B开始向上运动,从开始运动到A和B刚好分离的过程中,下列说法正确的是( )| A. | 要使A、B分离,场强大小至少应为$\frac{mg}{q}$ | |
| B. | 要使A、B分离,场强大小至少应为$\frac{2mg}{3q}$ | |
| C. | 物体B和弹簧组成的系统机械能一直减少 | |
| D. | 物体A和B组成的系统机械能先增大后减小 |
14.如图所示为两物体a、b从同一位置沿同一直线运动的速度图象,下列说法正确的是( )
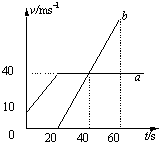

| A. | 第40s时,两物体a,b相遇 | |
| B. | 第60s时,两物体a,b相遇 | |
| C. | 第20s和第60s时,两物体a,b的间距相等 | |
| D. | a,b加速时,物体a的加速度大于物体b的加速度 |
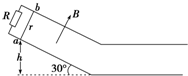 如图所示,两平行导轨间距L=0.1m,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接(连接处能量损失不计),倾斜部分与水平面间的夹角θ=30°,导轨的倾斜部分处于方向垂直斜面向上、磁感应强度B=0.5T的匀强磁场中,水平部分没有磁场.金属棒ab质量m=0.005kg、电阻r=0.02Ω,运动中与导轨始终接触良好,并且与导轨垂直,电阻R=0.08Ω,其余电阻不计,当金属棒从斜面上距地面高h=1.0m以上(含1.0m)任何地方由静止释放后,在水平面上滑行的最大距离x都是1.25m,取g=10m/s2.求:
如图所示,两平行导轨间距L=0.1m,足够长光滑的倾斜部分和粗糙的水平部分圆滑连接(连接处能量损失不计),倾斜部分与水平面间的夹角θ=30°,导轨的倾斜部分处于方向垂直斜面向上、磁感应强度B=0.5T的匀强磁场中,水平部分没有磁场.金属棒ab质量m=0.005kg、电阻r=0.02Ω,运动中与导轨始终接触良好,并且与导轨垂直,电阻R=0.08Ω,其余电阻不计,当金属棒从斜面上距地面高h=1.0m以上(含1.0m)任何地方由静止释放后,在水平面上滑行的最大距离x都是1.25m,取g=10m/s2.求: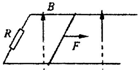 如图所示,一对平行光滑轨道放置在水平面上,两轨道相距L=1m,两轨道之间用电阻R=2Ω连接,有一质量为m=0.5kg的导体杆静止地放在轨道上与两轨道垂直,杆及轨道的电阻皆可忽略不计,整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上.现用水平拉力沿轨道方向拉导体杆,使导体杆从静止开始做匀加速运动.经过位移s=0.5m后,撤去拉力,导体杆又滑行了相同的位移s后停下.求:
如图所示,一对平行光滑轨道放置在水平面上,两轨道相距L=1m,两轨道之间用电阻R=2Ω连接,有一质量为m=0.5kg的导体杆静止地放在轨道上与两轨道垂直,杆及轨道的电阻皆可忽略不计,整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向上.现用水平拉力沿轨道方向拉导体杆,使导体杆从静止开始做匀加速运动.经过位移s=0.5m后,撤去拉力,导体杆又滑行了相同的位移s后停下.求: 如图,一根粗细均匀、内壁光滑、竖直放置的玻璃管下端密封,上端留有一抽气孔.管内下部被活塞封住一定量的气体(可视为理想气体),气体温度为T1开始时t将活塞上方的气体缓慢抽出,当活塞上方的压强达到po时,活塞下方气体的体积为V1,活塞上方玻璃管的容积为26V1活塞因重力而压强为0.5po继续将活塞上方抽成真空并密封整个抽气过程中管内气始终保持不变然后将密封的气体缓慢加热求:
如图,一根粗细均匀、内壁光滑、竖直放置的玻璃管下端密封,上端留有一抽气孔.管内下部被活塞封住一定量的气体(可视为理想气体),气体温度为T1开始时t将活塞上方的气体缓慢抽出,当活塞上方的压强达到po时,活塞下方气体的体积为V1,活塞上方玻璃管的容积为26V1活塞因重力而压强为0.5po继续将活塞上方抽成真空并密封整个抽气过程中管内气始终保持不变然后将密封的气体缓慢加热求: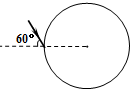 如图所示,一束单色光射入一半径为0.2m玻璃球体,入射角为60°,已知光线在玻璃球内经一次反射后,再次折射回到空气中时与入射光线平行.求:
如图所示,一束单色光射入一半径为0.2m玻璃球体,入射角为60°,已知光线在玻璃球内经一次反射后,再次折射回到空气中时与入射光线平行.求: