题目内容
1.如图甲所示,ab、cd为两根放置在同一水平面内且相互平行的金属轨道,相距L,右端连接一个阻值为R的定值电阻,轨道上放有一根导体棒MN,垂直两轨道且与两轨道接触良好,导体棒MN及轨道的电阻均可忽落不计.整个装置处于方向竖直向下的匀强磁场中,磁感应强度大小为B.导体棒MN在外力作用下以图中虚线所示范围的中心位置为平衡位置做简谐运动,其振动周期为T,振幅为A,在t=0时刻恰好通过平衡位置,速度大小为v0,其简谐运动的速度v随时间t按正弦规律变化,如图乙所示.则下列说法正确的是( )
| A. | 回路中电动势的瞬时值为BLv0sin$\frac{2π}{T}$t | |
| B. | 导体棒MN中产生交流电的功率为$\frac{{{B^2}{L^2}{v_0}^2}}{2R}$ | |
| C. | 通过导体棒MN的电流的有效值为$\frac{{\sqrt{2}BL{v_0}}}{R}$ | |
| D. | 在0~$\frac{T}{4}$内通过导体棒MN的电荷量为$\frac{{BL{v_0}T}}{8R}$ |
分析 导体棒MN做简谐运动,根据图象写出速度随时间的表达式,根据感应电动势公式E=BLv写出回路中电动势的瞬时值表达式.由有效值求出电功率.由平均值求出电量.
解答 解:A、导体棒速度的表达式v=v0cos$\frac{2π}{T}$t,回路中电动势的瞬时值:e=BLv=BLv0cos$\frac{2π}{T}$t,故A错误.
B、电动势的最大值为Em=BLv0,有效值为E=$\frac{\sqrt{2}{E}_{m}}{2}$=$\frac{\sqrt{2}}{2}$BLv0,导体棒MN中产生交流电的电功率P=$\frac{{E}^{2}}{R}$=$\frac{{B}^{2}{L}^{2}{v}_{0}^{2}}{2R}$,故B正确.
C、电流的有效值:I=$\frac{E}{R}$=$\frac{\sqrt{2}BL{v}_{0}}{2R}$.故C错误.
D、电量:q=$\overline{I}$△t=$\frac{\overline{E}}{R}$△t=$\frac{△Φ}{R△t}$△t=$\frac{△Φ}{R}$=$\frac{BLA}{R}$,故D错误;
故选:B.
点评 本题提供了产生正弦式交变电流的一种方式.交变电流求热量用有效值,求出电量用平均值.解题时要注意,求电功率时要用有效值,求电荷量时要应用法拉第电磁感应定律求出感应电动势,然后由欧姆定律求出电流,最后应用电流的定义式求出电荷量.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
5. 如图所示,在水平向右,场强为正的匀强磁场中,放一半径为R,原来不带电的金属球,G、F分别为球面上两点,且G、F连线与电场方向夹角为θ,GF=2R,则下面说法正确的是(其中图中A、B两点中有一点是接地的)( )
如图所示,在水平向右,场强为正的匀强磁场中,放一半径为R,原来不带电的金属球,G、F分别为球面上两点,且G、F连线与电场方向夹角为θ,GF=2R,则下面说法正确的是(其中图中A、B两点中有一点是接地的)( )
 如图所示,在水平向右,场强为正的匀强磁场中,放一半径为R,原来不带电的金属球,G、F分别为球面上两点,且G、F连线与电场方向夹角为θ,GF=2R,则下面说法正确的是(其中图中A、B两点中有一点是接地的)( )
如图所示,在水平向右,场强为正的匀强磁场中,放一半径为R,原来不带电的金属球,G、F分别为球面上两点,且G、F连线与电场方向夹角为θ,GF=2R,则下面说法正确的是(其中图中A、B两点中有一点是接地的)( )| A. | G、F两点的电势差为2REcosθ | B. | G、F两点处的场强都是水平向右 | ||
| C. | 如把球接地,则球可能带负电 | D. | 如把球接地,则球可能带正电 |
9.结合以下各选项中交代的情景及数据,下列判断正确的是( )
| A. | 位于点燃火药的坦克中的炮弹的速度、加速度可能均为零 | |
| B. | 轿车时速为100 km/h,紧急刹车阶段的加速度与速度反向 | |
| C. | 高速行驶的磁悬浮列车的加速度可能为零 | |
| D. | 刘翔在110m栏比赛中的成绩为13.07s,通过全程的平均速率为v=8.42m/s |
6.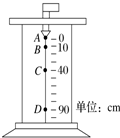 科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的间歇闪光灯的照射下,若调节间歇闪光时间间隔正好与水滴从A下落到B的时间相同,可以看到一种奇特的现象,水滴似乎不再下落,而是像固定在图中的A、B、C、D四个位置不动,对出现的这种现象,下列描述正确的是(g=10m/s2)( )
科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的间歇闪光灯的照射下,若调节间歇闪光时间间隔正好与水滴从A下落到B的时间相同,可以看到一种奇特的现象,水滴似乎不再下落,而是像固定在图中的A、B、C、D四个位置不动,对出现的这种现象,下列描述正确的是(g=10m/s2)( )
 科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的间歇闪光灯的照射下,若调节间歇闪光时间间隔正好与水滴从A下落到B的时间相同,可以看到一种奇特的现象,水滴似乎不再下落,而是像固定在图中的A、B、C、D四个位置不动,对出现的这种现象,下列描述正确的是(g=10m/s2)( )
科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的间歇闪光灯的照射下,若调节间歇闪光时间间隔正好与水滴从A下落到B的时间相同,可以看到一种奇特的现象,水滴似乎不再下落,而是像固定在图中的A、B、C、D四个位置不动,对出现的这种现象,下列描述正确的是(g=10m/s2)( )| A. | 水滴在下落过程中通过相邻两点之间的时间满足tAB<tBC<tCD | |
| B. | 间歇发光的间隔时间是$\frac{\sqrt{2}}{10}$ s | |
| C. | 水滴在相邻两点之间的位移满足xAB:xBC:xCD=1:3:5 | |
| D. | 水滴在各点速度之比满足vB:vC:vD=1:4:9 |
11.2002年2月“哥伦比亚号”航天飞机在进飞地球高空大气层时,发生意外事故,7名宇航员全部遇难,该航天飞机进入大气层时与地面成45°夹角,发生事故后,动力关闭,该飞机的运动状态为( )
| A. | 沿原方向做匀速直线运动 | |
| B. | 做自由落体运动 | |
| C. | 做曲线运动 | |
| D. | 由于空气阻力,飞机可能做直线运动,也可能做曲线运动 |
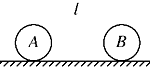 如图所示,质量均为m的两个带电小球A和B放置在光滑的绝缘水平面上,彼此相距为l,A球带电荷量+Q,B球带电荷量-Q,若用一水平力拉动其中一个球,且要使另一个球与前面的球始终保持l的间距运动,则拉力F的大小为?
如图所示,质量均为m的两个带电小球A和B放置在光滑的绝缘水平面上,彼此相距为l,A球带电荷量+Q,B球带电荷量-Q,若用一水平力拉动其中一个球,且要使另一个球与前面的球始终保持l的间距运动,则拉力F的大小为?