��Ŀ����
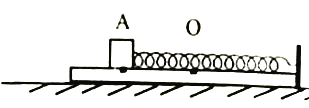
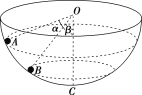
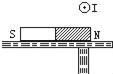
����Ŀ����ͼ��ʾ��������ͬ�İ�Բ�ι⻬��Ե����ֱ���ֱ��������ǿ�糡E����ǿ�ų�B�У����������ͬһ�߶��ϣ�������ͬ�Ĵ�����С��a��bͬʱ�ӹ�������ߵ��ɾ�ֹ�ͷţ������˶���ʼ�����ع��ͨ�����Թ������͵�M��N��������
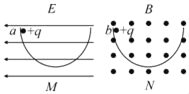
A. ��С��ij�ε�������͵�ʱ���ٶȴ�С��������vN=vM
B. ��С���ܵ����������Ҷ�
C. С��a��b��һ��ͬʱ������͵�
D. ��һ�ε�������͵�ʱ��С��a�Թ����ѹ��С��С��b�Թ����ѹ��
���𰸡�AD
��������
С���ڴų����˶�������������С������������������С��Ļ�е���غ㣬С���ڵ糡���ܵ��ĵ糡����С����������������͵�ʱ���ٶȴ�С��С����������İ뾶��ͬ������Բ���˶����������Ĺ�ʽ���Է���С��ͨ����͵��ǶԹ����ѹ����
��С���ڴų����˶�������������С������������������С��Ļ�е���غ㣻��С���ڵ糡���˶�ʱ�糡����С����������������͵�ʱ���ٶȵĴ�С��С�����Բ�������vN=vM��һ����vN��vM�����ڵ糡���˶���ʱ��Ҳ������A��ȷ��C��������С���ڴų����˶�������������С��Ļ�е���غ㣬����С����Ե���������һ�ˣ����糡����С��������������С���ڴﵽ�����һ��֮ǰ�ٶȾͼ�Ϊ���ˣ��ʲ��ܵ������Ҷˣ���B����С���ڴų����˶�������͵��������������֪��![]() ����ã�
����ã�![]() ��С���ڵ糡���˶�������͵�����������֪��
��С���ڵ糡���˶�������͵�����������֪�� ![]() ����ã�
����ã�![]() ����ΪvN��vM����FN��FM������ţ�ٵ�������֪��С��a�Թ����ѹ��С��С��b�Թ����ѹ������D��ȷ������AD��ȷ��BC����
����ΪvN��vM����FN��FM������ţ�ٵ�������֪��С��a�Թ����ѹ��С��С��b�Թ����ѹ������D��ȷ������AD��ȷ��BC����

 Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�