题目内容
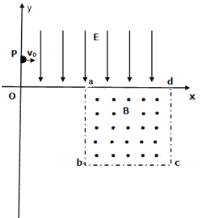
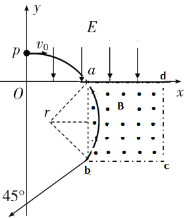
【题目】如图，质量为M的足够长金属导轨abcd放在光滑的绝缘水平面上。一电阻不计，质量为m的导体棒PQ放置在导轨上，始终与导轨接触良好，PQbc构成矩形。棒与导轨间动摩擦因数为μ，棒左侧有两个固定于水平面的立柱。导轨bc段长为L，开始时PQ左侧导轨的总电阻为R，右侧导轨单位长度的电阻为R0。以ef为界，其左侧匀强磁场方向竖直向上，右侧匀强磁场水平向左，磁感应强度大小均为B。在t=0时，一水平向左的拉力F垂直作用于导轨的bc边上，使导轨由静止开始做匀加速直线运动，加速度为a。
(1)求导轨刚开始运动时拉力F的大小；
(2)求导轨运动时间足够长后拉力F的渐近值及整个过程中拉力F的最大值；
(3)若某一过程中导轨动能的增加量为△Ek，导轨克服摩擦力做功为W，求回路产生的焦耳热。
【答案】（1）
（2）
（3）
【解析】（1）导轨刚开始运动时对导轨有：
解得：
（2）导轨运动以后
得：
对导轨由牛顿第二定律有：
又有
由公式可得;
分析可知：当t趋于无穷大时，
当
时，
（3）对框架在加速过程中由动能定理知：
则：
又
则
解得：
故本题答案是：（1）（2）（3）
练习册系列答案
相关题目
