题目内容
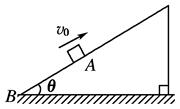
(12分)如图所示,足够长的斜面固定在地面上,倾角θ=37°,一物体以v0=12 m/s的初速度,从斜面A点处沿斜面向上运动.加速度大小为a=8.0 m/s2.已知重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8.求:
(1)物体沿斜面上滑的最大距离x;
(2)物体与斜面间的动摩擦因数μ;
(3)物体沿斜面到达最高点后下滑返回A点时的速度大小v.

(1)物体沿斜面上滑的最大距离x;
(2)物体与斜面间的动摩擦因数μ;
(3)物体沿斜面到达最高点后下滑返回A点时的速度大小v.
(1)9 m (2)0.25 (3) 6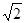 m/s
m/s
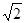 m/s
m/s试题分析:(1)由
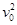 =2ax得
=2ax得x=
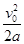 =
=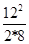 m=9 m. 2分
m=9 m. 2分(2)物体上滑时受力情况如图甲所示.
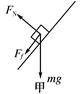
则由牛顿第二定律得
沿斜面方向上:mgsinθ+Ff=ma ① 2分
垂直斜面方向上:mgcos θ-FN=0 ② 1分
又:Ff=μFN. ③ 1分
由①②③式解得:μ=0.25. 1分
(3)物体沿斜面下滑时受力情况如右图乙所示
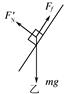
由牛顿第二定律得
沿斜面方向上:mgsin θ-F′f=ma′ ④ 2分
垂直斜面方向上:mgcos θ-F′N=0 ⑤
又:F′f=μF′N ⑥
由④⑤⑥式代入数据解得:a′=4 m/s2. 2分
由v2=2a′x 得v=6
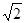 m/s 1分
m/s 1分点评:难度中等,加速度为联系运动和力的桥梁,如果要判断受力,应先根据运动情况求得加速度,再由受力和牛顿第二定律求解,在第二问中,思路正好相反

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目

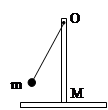
 的加速度竖直加速上升时,细绳对物体的拉力是( )
的加速度竖直加速上升时,细绳对物体的拉力是( )