��Ŀ����
����Ŀ����ͼ��ʾ�����Ϊ37o�Ĵֲ�б��̶���ˮƽ�����ϣ�б���Ϸ���������Ϊ1kg��A��B�����壬A��B֮����һ����ϵ���ܴ�����ʵ��ɣ�������A˨������B�Ӵ�����˨������ʼ���ɱ���������������Ϊ4J��A��Bǡ�þ�ֹ��б���ϣ�������б�������Ħ�����뻬��Ħ������ȣ�B��б���Ķ�Ħ��������A��2�����ֽ������������A��B�ڼ��̵�ʱ���ڱ����ɵ�������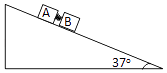
��1��A��B��б����Ħ������u1��u2�ֱ��Ƕ��٣�
��2�����ɸջָ�ԭ��ʱA��B���ٶȴ�Сv1��v2
��3�����ɸջָ�ԭ����1.2sʱ��A��B��ľ��룮
���𰸡�
��1���⣺A��Bǡ�þ�ֹ��б���ϣ�������ܵ���Ħ�����ĺ͵���������б�����µķ�����u1mgcos37��+u2mgcos37��=2mgsin37��
�֣�2u1=u2
�����ã�u1=0.5��u2=1
��A��B��б����Ħ������u1��u2�ֱ���0.5��1
��2���⣺����A��B�ڼ��̵�ʱ���ڱ����ɵ�����������Ϊ�����ڷֿ��Ĺ�������б�淽��Ķ����غ㣬�ã�mv1=mv2
�֣�Ep= ![]() mv12+
mv12+ ![]() mv22
mv22
�����ã�v1=2m/s��v2=2m/s
�𣺵��ɸջָ�ԭ��ʱA��B���ٶȴ�С����2m/s��
��3���⣺A�����˶�ʱ��mgsin37��+u1mgcos37��=ma1
�ã�a1=10m/s2
�����˶���ʱ�䣺t1= ![]() s
s
���ϵ�λ�ƣ�x1= ![]() v1 t1=
v1 t1= ![]() =0.2m
=0.2m
A�����˶�ʱ��������Ϊ������mgsin37�㩁u1mgcos37��=ma2
�ã�a2=2m/s2
�˶���ʱ�䣺t2=1.2��t1=1s
�����˶���λ�ƣ�x2= ![]() a2t22=
a2t22= ![]() =1m
=1m
B�����˶�ʱ��mgsin37�㩁u2mgcos37��=ma
�ã�a=��2m/s2
t= ![]() =1s��1.2s
=1s��1.2s
x= ![]() =1m
=1m
����֮��ľ��룺��x=x����x2��x1��=1����1��0.2��=0.2m
�𣺵��ɸջָ�ԭ����1.2sʱ��A��B��ľ�����0.2m��
����������1����ʼʱA��Bǡ�þ�ֹ��б���ϣ�����������������Ϲ�����ƽ������������������2�����ݶ����غ㣬��Ϲ��ܹ�ϵ�����������3���ֱ�����ǽ���������������ţ�ٵڶ�����������Եļ��ٶȣ�Ȼ�����˶�ѧ�Ĺ�ʽ���������
�����㾫���������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ�Ͷ����غ㶨���ǽ����ĸ�������Ҫ֪���ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ�������غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮