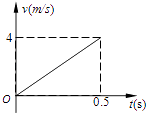��Ŀ����
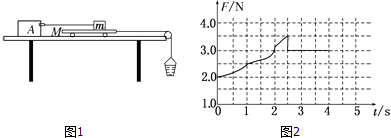
����Ŀ��һ��ƽ��С�����ڹ⻬ˮƽ���ϣ����Ҷ�ǡ�ú�һ�� ![]() �⻬Բ�����AB�ĵ˵ȸ����ӣ���ͼ��ʾ����֪С������M=3.0kg����L=2.06m��Բ������İ뾶R=0.8m���ֽ�һ����m=1.0kg��С�����ɹ������A�������ͷţ����黬��B�˺����С����������С���ϱ����Ķ�Ħ��������=0.3��g=10m/s2 ��
�⻬Բ�����AB�ĵ˵ȸ����ӣ���ͼ��ʾ����֪С������M=3.0kg����L=2.06m��Բ������İ뾶R=0.8m���ֽ�һ����m=1.0kg��С�����ɹ������A�������ͷţ����黬��B�˺����С����������С���ϱ����Ķ�Ħ��������=0.3��g=10m/s2 �� 
��1�����鵽��B�ˣ��������֧�����Ĵ�С��
��2��С���˶�1.5sʱ�����Ҷ˾���B�˵ľ��룻
��3�������복�������Ħ�������������ܣ�
���𰸡�
��1���⣺���ݶ��ܶ����ã� ![]()
���v2=2gR��v= ![]()
��B����N��mg= ![]() �����N=3mg=30N��
�����N=3mg=30N��
�ʻ��鵽��B�ˣ��������֧�����Ĵ�СΪ30N��
��2���⣺С���ļ��ٶ� ![]() ��
��
����ļ��ٶ� ![]()
�������ٶ����ʱ�У�a1t0=v��a2t0
��� ![]()
֪С����1.5s�������ȼ���ֱ���˶���Ȼ��������ֱ���˶���
�ȼ���ֱ���˶���λ�� ![]()
����ֱ���˶����ٶ�v��=a1t0=1��1m/s=1m/s
������ֱ���˶���λ��x2=v��t��=0.5m
����x=x1+x2=1m
��С���˶�1.5sʱ�����Ҷ˾���B�˵ľ���Ϊ1m��
��3���⣺�����߹�ͬ�ٶ�Ϊv1�����ݶ����غ㶨�ɵã�mv=��M+m��v1
��� ![]()
���������غ�ã�Q= ![]()
�ʻ����복�������Ħ��������������Ϊ6J��
����������1�����ݶ��ܶ������С�����A���˶���B����ٶȣ�����ţ�ٵڶ�����������������֧��������2�����黬��С����С�����ȼ���ֱ���˶����������ȼ���ֱ���˶����������ٶ����ʱ��һ��������ֱ���˶����ж�1.5sʱ��������С���ٶ��Ƿ���ȣ�Ȼ��ͨ���˶�ѧ��ʽ������Ҷ˾���B�˵ľ��룮��3�����ݶ����غ㶨���������ͳ��Ĺ�ͬ�ٶȣ�Ȼ��ͨ�������غ㶨�����Ħ�������������ܣ�
�����㾫�������ö��ܶ������ۺ�Ӧ�úͶ����غ㶨�ɶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ������غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮