题目内容
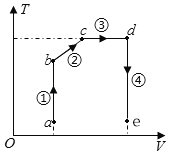
【题目】如图，a、b、c、d为光滑斜面上的四个点。一小滑块自a点由静止开始下滑，通过ab、bc、cd各段所用时间均为T。现让该滑块自b点由静止开始下滑，则该滑块( )
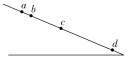
A. 通过bc、cd段的时间均大于T
B. 通过c、d点的速度之比为1∶2
C. 通过bc、cd段的位移之比为1∶3
D. 通过c点的速度等于通过bd段的平均速度
【答案】A
【解析】
质点从a点由静止开始下滑，经光滑斜面上的三段位移时间相等，运用初速度为零的匀加速直线运动的比例式进行分析，结合匀变速直线运动的规律分析．
当滑块由a点静止下滑时，滑块沿光滑的斜面做匀加速直线运动，加速度大小为a′。假设ab段的间距为x，则bc段、cd段的间距应分别为3x、5x，xbc∶xcd＝3∶5，C错误；如果滑块由b点静止释放，显然滑块通过bc段、cd段的时间均大于T，A正确；滑块在c点的速度应为v1＝
，滑块在d点的速度应为v2＝
，则v1∶v2＝
，B错误；因为xbc∶xcd＝3∶5，显然通过c点的时刻不是bd的中间时刻，则滑块通过c点的速度不等于bd段的平均速度，D错误。故选A.
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
