��Ŀ����
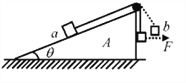
����Ŀ����ͼ��ʾ��һ��ΪL��ֱ��AB��ˮƽ��ɦ��ǹ̶����ڸ�����һ����Ϊm��С���飬�˵�B����һ���Ե��壬������洹ֱ�������뵲����ײ����ԭ���ʷ��أ��ֽ���������A���ɾ�ֹ�ͷţ������뵲���һ����ײ��ǡ����������AB���е㣬�������ٶ�Ϊg���ɴ˿���ȷ���� ��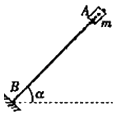
A.�����»�ʱ���ٶȵĴ�С
B.�������֮��Ķ�Ħ������
C.�������ս�ͣ�ڸ˵ĵ�
D.�����һ���»����õ�ʱ��
���𰸡�A,B,C
���������⣺AB����AB=L�����������̣��ɶ��ܶ����ã�mg ![]() sin������mgcos����L+
sin������mgcos����L+ ![]() ��=0����� ��=
��=0����� ��= ![]() tan��������ȷ���������֮��Ķ�Ħ��������
tan��������ȷ���������֮��Ķ�Ħ��������
�»����̣�����ţ�ٵڶ����ɵ� mgsin������mgcos��=ma����� a=gsin������gcos��������ȷ�������»�ʱ���ٶȵĴ�С����AB��ȷ��
C������ɵã�mgsin������mgcos������֪���鲻�ܾ�ֹ��AB���е㣬�����»�����Ϊ���˴ֲڣ�����Ļ�е�ܲ�����ʧ���������ջ���ͣ�ڸ˵ĵˣ���C��ȷ��
D�����ڵ�һ���»����̣���λ�ƹ�ʽ�� L= ![]() ������Lδ֪�����Բ�����������һ���»����õ�ʱ�䣬��D����
������Lδ֪�����Բ�����������һ���»����õ�ʱ�䣬��D����
��ѡ��ABC
�����㾫����ͨ��������ö��ܶ��������⣬���ն��ܶ����ı���ʽ���������ܺ�����������ֱ���˶�������µó���.����Ҳ�����ڱ����������������˶�����������Ͷ��ܶ��DZ�������������ʸ������ֽ⣬�ʶ��ܶ�������ʽ�����Խ����⣮

 ��У����ϵ�д�
��У����ϵ�д�