题目内容
7.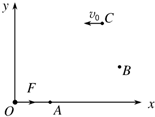 如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、O两点距离为a,在A点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求:
如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、O两点距离为a,在A点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求:(1)质点到达B点的速度大小及方向;
(2)C点到X轴的距离.
分析 (1)质点从O到A做匀加速直线运动,从A到B做类平抛运动,从B到C做匀速圆周运动,由几何关系得出AB的距离,进而可得B点的速度方向与x轴夹角;
(2)B到C点做匀速圆周运动,依据向心力表达式可表示半径,从OA段的运动可以表示圆周运动的速度,联立可的半径大小,由几何关系可得C点与x轴的距离.
解答 解:(1)从O到A物体做匀加速运动,到达A点的速度满足${v}^{2}=2\frac{F}{m}a$;
从A到B,物体在x方向做匀速运动,在y方向做匀加速运动,所以AB的水平距离为2a,竖直距离为a,A、B两点距离为$\sqrt{5}$a;
在B点的x方向的速度等于沿y方向的速度均等于v,
所以在B点的速度方向与x轴夹角为45°,
大小等于$\sqrt{2}$v=$\frac{2\sqrt{2}}{t}a$
(2)由B到C质点做匀速圆周运动4F=$\frac{m(\sqrt{2}v)^{2}}{r}$,
求得r=a.所以C点与x轴的距离为r+rsin45°+a=$\frac{4+\sqrt{2}}{2}a$;
答:(1)质点到达B点的速度大小$\frac{2\sqrt{2}}{t}a$及方向与x轴夹角为45°;
(2)C点到X轴的距离$\frac{4+\sqrt{2}}{2}a$.
点评 解决本题的关键知道质点经历了匀加速直线运动,类平抛运动,匀速圆周运动,结合运动学公式灵活求解.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 肥皂膜在阳光的照射下呈现彩色是光的干涉现象造成的 | |
| B. | 根据麦克斯韦电磁理论,变化的磁场一定能产生变化的电场 | |
| C. | X射线在电场中能够发生偏转 | |
| D. | 波的频率与振源的频率相同 |
19.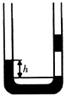 如图所示,两端开口的U型管中装有水银,在右管中用水银封闭着一段空气,要使两侧水银面高度差h增大,应( )
如图所示,两端开口的U型管中装有水银,在右管中用水银封闭着一段空气,要使两侧水银面高度差h增大,应( )
 如图所示,两端开口的U型管中装有水银,在右管中用水银封闭着一段空气,要使两侧水银面高度差h增大,应( )
如图所示,两端开口的U型管中装有水银,在右管中用水银封闭着一段空气,要使两侧水银面高度差h增大,应( )| A. | 从左管滴入水银 | B. | 从右管滴入水银 | C. | 让气体升温 | D. | 增大大气压强 |
16.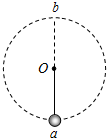 如图所示,长度为L的轻质细杆的一端与质量为m的小球相连,可绕过O点的水平轴自由转动.现在最低点给小球一水平初速度v0,使它能在竖直平面内做圆周运动.设小球在轨道最低点a和最高点b受到细杆的作用力大小分别为F1和F2,重力加速度为g,则下列判断正确的是( )
如图所示,长度为L的轻质细杆的一端与质量为m的小球相连,可绕过O点的水平轴自由转动.现在最低点给小球一水平初速度v0,使它能在竖直平面内做圆周运动.设小球在轨道最低点a和最高点b受到细杆的作用力大小分别为F1和F2,重力加速度为g,则下列判断正确的是( )
 如图所示,长度为L的轻质细杆的一端与质量为m的小球相连,可绕过O点的水平轴自由转动.现在最低点给小球一水平初速度v0,使它能在竖直平面内做圆周运动.设小球在轨道最低点a和最高点b受到细杆的作用力大小分别为F1和F2,重力加速度为g,则下列判断正确的是( )
如图所示,长度为L的轻质细杆的一端与质量为m的小球相连,可绕过O点的水平轴自由转动.现在最低点给小球一水平初速度v0,使它能在竖直平面内做圆周运动.设小球在轨道最低点a和最高点b受到细杆的作用力大小分别为F1和F2,重力加速度为g,则下列判断正确的是( )| A. | 若v0>$\sqrt{5gL}$,则v0越大,F1和F2之差越大 | |
| B. | 若v0>$\sqrt{5gL}$,F1和F2之差为定值,与v0的大小无关 | |
| C. | 若v0<$\sqrt{5gL}$,则v0越小,F1和F2之和越小 | |
| D. | 若v0<$\sqrt{5gL}$,F1和F2之和为定值,与v0的大小无关 |
17.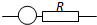 一电压表由电流表G与电阻R串联而成,如图所示,若在使用中发现此电压表的读数总比准确值稍小一些,采用下列哪种措施可能加以改进( )
一电压表由电流表G与电阻R串联而成,如图所示,若在使用中发现此电压表的读数总比准确值稍小一些,采用下列哪种措施可能加以改进( )
 一电压表由电流表G与电阻R串联而成,如图所示,若在使用中发现此电压表的读数总比准确值稍小一些,采用下列哪种措施可能加以改进( )
一电压表由电流表G与电阻R串联而成,如图所示,若在使用中发现此电压表的读数总比准确值稍小一些,采用下列哪种措施可能加以改进( )| A. | 在R上串联一比R小得多的电阻 | B. | 在R上串联一比R大得多的电阻 | ||
| C. | 在R上并联一比R小得多的电阻 | D. | 在R上并联一比R大得多的电阻 |
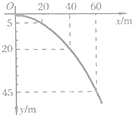 某研究小组在做平抛物体的运动实验时,取水平方向为x轴,正方向与初速度v的方向相同,取竖直方向为y轴,正方向向下,取抛出点为坐标原点,描绘出物体做平抛运动的轨迹如图所示,可求出v=20m/s.
某研究小组在做平抛物体的运动实验时,取水平方向为x轴,正方向与初速度v的方向相同,取竖直方向为y轴,正方向向下,取抛出点为坐标原点,描绘出物体做平抛运动的轨迹如图所示,可求出v=20m/s.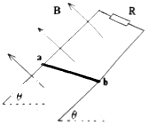 如图所示,足够长的U形光滑金属导轨平面与水平面成θ角,与磁感应强度为B的匀强磁场垂直,导轨间距为L,上端与电阻为R连接,导轨电阻不计,ab棒的质量为m,连接电路的电阻为r,金属棒ab由静止开始沿导轨下滑,并与两导轨始终垂直且接触良好,当电阻R上产生的电热为Q时金属棒ab恰好达到最大速度,求:
如图所示,足够长的U形光滑金属导轨平面与水平面成θ角,与磁感应强度为B的匀强磁场垂直,导轨间距为L,上端与电阻为R连接,导轨电阻不计,ab棒的质量为m,连接电路的电阻为r,金属棒ab由静止开始沿导轨下滑,并与两导轨始终垂直且接触良好,当电阻R上产生的电热为Q时金属棒ab恰好达到最大速度,求: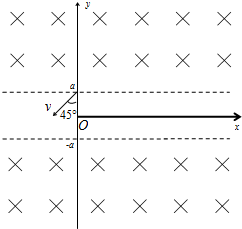 在如图所示的xoy平面直角坐标系中,一足够长绝缘薄板正好和x轴的正半轴重合,在y>a和y<-a的区域内均分布着方向垂直纸面向里的相同的匀强磁场.一带正电粒子,从y轴上的(0,a)点以速度v沿与y轴负向成45°角出射.带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变.已知粒子质量为m,电荷量为q,磁感应强度的大小B=$\frac{\sqrt{2}mv}{4qa}$.不计粒子的重力.
在如图所示的xoy平面直角坐标系中,一足够长绝缘薄板正好和x轴的正半轴重合,在y>a和y<-a的区域内均分布着方向垂直纸面向里的相同的匀强磁场.一带正电粒子,从y轴上的(0,a)点以速度v沿与y轴负向成45°角出射.带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变.已知粒子质量为m,电荷量为q,磁感应强度的大小B=$\frac{\sqrt{2}mv}{4qa}$.不计粒子的重力. 如图所示,一个横截面为直角三角形的三棱镜,∠C=90°.一条与BC面成θ=30°角的光线斜射向BC面,第一次经AC面时即刚好发生全反射.求:该棱镜材料的折射率n.
如图所示,一个横截面为直角三角形的三棱镜,∠C=90°.一条与BC面成θ=30°角的光线斜射向BC面,第一次经AC面时即刚好发生全反射.求:该棱镜材料的折射率n.