题目内容
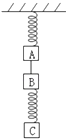
【题目】如图，物块a、b和c的质量相同，a和b、b和c之间用完全相同的轻弹簧S1和S2相连，通过系在a上的细线悬挂于固定点O．整个系统处于静止状态．现将细线剪断．将物块a的加速度的大小记为a1 ， S1和S2相对于原长的伸长分别记为△l1和△l2 ， 重力加速度大小为g．在剪断的瞬间，（ ）
A.a1=3g
B.a1=0
C.△l1=2△l2
D.△l1=△l2
【答案】A,C
【解析】解：A、B、对a、b、c分别受力分析如图，
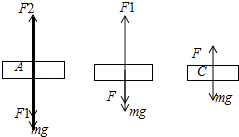
根据平衡条件，有：
对a：F2=F1+mg
对b：F1=F+mg
对c：F=mg
所以：F1=2mg
弹簧的弹力不能突变，因形变需要过程，绳的弹力可以突变，绳断拉力立即为零．
当绳断后，b与c受力不变，仍然平衡，故a=0；
对a，绳断后合力为F合=F1+mg=3mg=maa，aa=3g方向竖直向下；故A正确，B错误．
C、D、当绳断后，b与c受力不变，则F1=k△l1， 
；同时：F=k△l2，所以： 
．联立得△l1=2△l2：故C正确，D错误．
故选：AC．
对细线剪短前后的a、b、c物体分别受力分析，然后根据牛顿第二定律求解加速度与弹簧的伸长量．
练习册系列答案
相关题目
