题目内容
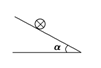
(10分)如图所示,处于匀强磁场中的两根光滑足够长、电阻不计的平行金属导轨相距1 m,导轨平面与水平面成θ=37°角,上端连接阻值为R=2 Ω的电阻.匀强磁场方向与导轨平面垂直,磁感应强度B=0.4 T。质量m=0.2 kg、电阻r=1 Ω的金属棒ab,以初速度v0从导轨底端向上滑行,金属棒ab在安培力和一平行于导轨平面的外力F的共同作用下做匀变速直线运动,加速度大小为a=3 m/s2、方向和初速度方向相反,在金属棒运动过程中,电阻R消耗的最大功率为1.28 W。设金属棒与导轨垂直并保持良好接触(g=10 m/s2,sin 37°=0.6,cos 37°=0.8)。求:

(1)金属棒产生的感应电动势的最大值;
(2)金属棒初速度v0的大小;
(3)当金属棒速度的大小为初速度一半时施加在金属棒上外力F的大小和方向。

(1)金属棒产生的感应电动势的最大值;
(2)金属棒初速度v0的大小;
(3)当金属棒速度的大小为初速度一半时施加在金属棒上外力F的大小和方向。
(1)2.4 V (2)6 m/s (3)0.76 N 沿导轨平面向上或0.44 N 沿导轨平面向上
(1)(2分)当电阻R消耗的功率最大时,感应电动势最大,
则Im= =
= A=0.8 A
A=0.8 A
Em=Im(R+r)=0.8×(2+1) V=2.4 V.
(2)(2分)因为加速度方向与初速度方向相反,所以在上滑过程中,初速度为最大速度,即Em=Blv0
则v0= =6 m/s.
=6 m/s.
(3)(6分)当v=3 m/s时,F安= =0.16 N
=0.16 N
分两种情况讨论
①在上升过程中,由牛顿第二定律得
Gx+F安-F外=ma
F外=0.76 N
方向沿导轨平面向上.
②在下降过程中,
Gx-F安-F外=ma
F外=0.44 N
方向沿导轨平面向上.
则Im=
 =
= A=0.8 A
A=0.8 A Em=Im(R+r)=0.8×(2+1) V=2.4 V.
(2)(2分)因为加速度方向与初速度方向相反,所以在上滑过程中,初速度为最大速度,即Em=Blv0
则v0=
 =6 m/s.
=6 m/s. (3)(6分)当v=3 m/s时,F安=
 =0.16 N
=0.16 N分两种情况讨论
①在上升过程中,由牛顿第二定律得
Gx+F安-F外=ma
F外=0.76 N
方向沿导轨平面向上.
②在下降过程中,
Gx-F安-F外=ma
F外=0.44 N
方向沿导轨平面向上.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目