题目内容
【题目】如图所示，在竖直平面内有一半径为R的圆弧轨道，半径OA水平、OB竖直，一个质量为m的小球自A的正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力．已知AP=2R，重力加速度为g，则小球从P到B的运动过程中（ ）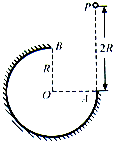
A.重力做功mgR
B.机械能减少mgR
C.合外力做功mgR
D.克服摩擦力做功0.5mgR
【答案】A,D
【解析】解：A、重力做功WG=mg（2R﹣R）=mgR，A符合题意；
B、小球沿轨道到达最高点B时恰好对轨道没有压力，则有
mg=m 
，解得：vB= 
则机械能减少量为△E=mgR﹣ 
=0.5mgR，B不符合题意．
C、根据动能定理得：
合外力做功 W合= 
mvB2=0.5mgR，C不符合题意．
D、根据功能原理可知，克服摩擦力做功等于机械能的减少，为0.5mgR．D符合题意．
故选：AD．
【考点精析】通过灵活运用功能关系和动能定理的综合应用，掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1；应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷即可以解答此题．
【题目】在做“研究匀变速直线运动”的实验时，某同学得到一条用电火花计时器打下的纸带如图甲所示，并在其上取了A、B、C、D、E、F、G 7个计数点，每相邻两个计数点间还有4个点图中没有画出，电火花计时器接220V、50Hz交流电源．他经过测量并计算得到电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表：
对应点 | B | C | D | E | F |
速度（m/s） | 0.141 | 0.185 | 0.220 | 0.254 | 0.301 |
（1）设电火花计时器的周期为T，计算vF的公式为vF=；
（2）根据（1）中得到的数据，以A点对应的时刻为t=0，试在图乙所示坐标系中合理地选择标度，作出v﹣t图象．
（3）利用该图象求物体的加速度a=m/s2；（结果保留2位有效数字）
（4）如果当时电网中交变电流的电压变成210V，而做实验的同学并不知道，那么加速度的测量值与实际值相比（选填：“偏大”、“偏小”或“不变”）．
