Question

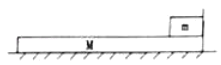
【题目】如图所示，质量为2kg的木板M放置在足够大光滑水平面上，其右端固定一轻质刚性竖直挡板，能承受的最大压力为4N，质量为1kg的可视为质点物块m恰好与竖直挡板接触，已知M、m间动摩擦因数=0.5，假设最大静摩擦力等于滑动摩擦力。初始两物体均静止，某时刻开始M受水平向左力F作用，F与M位移关系为F=3+0.5x，重力加速度g=10m/s2，关于M、m的运动，下列表述正确的是（ ）

A.m的最大加速度为5m/s2

B.m获得的最大速度无法求解

C.当F刚作用时，竖直挡板对m就有弹力作用

D.当M运动位移为24m过程中，F所做的功为216J

Answer 1

【答案】D

【解析】

A．m与木板M之间的最大静摩擦力为

N＝5N

m受到的向左的力最大为静摩擦力与弹力的和，所以最大加速度为

am==m/s2=9m/s2

故A错误；

BC．开始时m与木板一起做加速运动，共同的加速度为

a===1+x

刚开始时，x=0，则加速度为a0=1m/s2。开始时m受到的摩擦力为

N=1N＜5N

所以当F刚作用时，竖直挡板对m没有弹力作用；由am=9m/s2和=1+x，可知当m的加速度最大时的位移为xm=48m，根据F的平均值可求出拉力对系统做的功，由动能定理即可求出系统的动能，即

由此即可求出m的最大速度，故BC错误；

D．当M运动位移为24m时有

F=3+0.5×24N=15N

根据功的公式有

可知力F做的功等于力在空间的积累效果，由积累的关系可得

W=x=×24J=216J

故D正确。

故选D。